
Question Number 177688 by mathlove last updated on 08/Oct/22
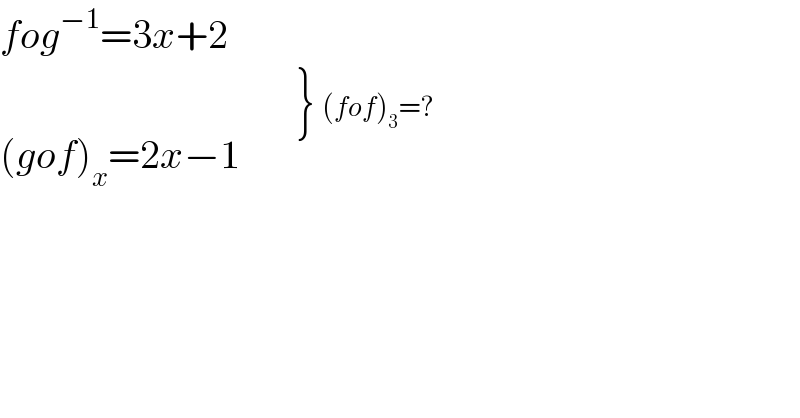
$${fog}^{−\mathrm{1}} =\mathrm{3}{x}+\mathrm{2} \\ $$$$\left({gof}\right)_{{x}} =\mathrm{2}{x}−\mathrm{1}\:\:\:\:\:\overset{\left.\begin{matrix}{}\\{}\end{matrix}\right\}\:\:\left({fof}\right)_{\mathrm{3}} =?} {\:} \\ $$
Commented by cortano1 last updated on 08/Oct/22
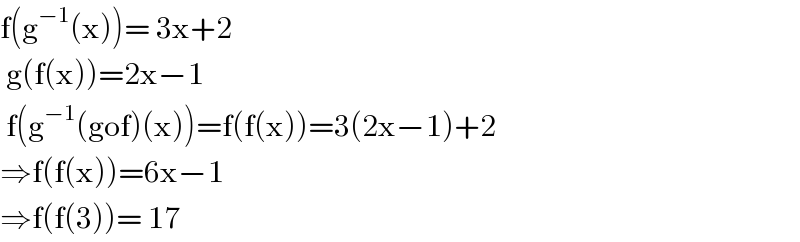
$$\mathrm{f}\left(\mathrm{g}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)=\:\mathrm{3x}+\mathrm{2} \\ $$$$\:\mathrm{g}\left(\mathrm{f}\left(\mathrm{x}\right)\right)=\mathrm{2x}−\mathrm{1} \\ $$$$\:\mathrm{f}\left(\mathrm{g}^{−\mathrm{1}} \left(\mathrm{gof}\right)\left(\mathrm{x}\right)\right)=\mathrm{f}\left(\mathrm{f}\left(\mathrm{x}\right)\right)=\mathrm{3}\left(\mathrm{2x}−\mathrm{1}\right)+\mathrm{2} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{f}\left(\mathrm{x}\right)\right)=\mathrm{6x}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{f}\left(\mathrm{3}\right)\right)=\:\mathrm{17} \\ $$
Commented by mathlove last updated on 09/Oct/22

$${thanks} \\ $$
