
Question Number 17748 by ibraheem160 last updated on 10/Jul/17
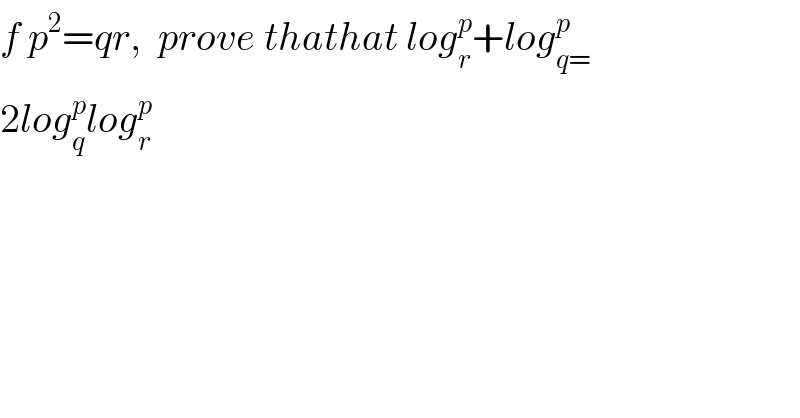
$${f}\:{p}^{\mathrm{2}} ={qr},\:\:{prove}\:{thathat}\:{log}_{{r}} ^{{p}} +{log}_{{q}=} ^{{p}} \\ $$$$\mathrm{2}{log}_{{q}} ^{{p}} {log}_{{r}} ^{{p}} \\ $$
Commented by tawa tawa last updated on 10/Jul/17
![((logp)/(logr)) + ((logp)/(logq)) = ((logplogq + logplogr)/(logrlogq)) = ((logp[logq + logr])/(logrlogq)) = ((logp(logqr))/(logrlogq)) from p^2 = qr = ((logplogp^2 )/(logrlogq)) = ((logp)/(logr)) × ((logp^2 )/(logq)) = log_r p × 2log_q p = 2log_q plog_r p QED](Q17752.png)
$$\frac{\mathrm{logp}}{\mathrm{logr}}\:+\:\frac{\mathrm{logp}}{\mathrm{logq}} \\ $$$$=\:\frac{\mathrm{logplogq}\:+\:\mathrm{logplogr}}{\mathrm{logrlogq}} \\ $$$$=\:\frac{\mathrm{logp}\left[\mathrm{logq}\:+\:\mathrm{logr}\right]}{\mathrm{logrlogq}} \\ $$$$=\:\frac{\mathrm{logp}\left(\mathrm{logqr}\right)}{\mathrm{logrlogq}} \\ $$$$\mathrm{from}\:\:\mathrm{p}^{\mathrm{2}} \:=\:\mathrm{qr} \\ $$$$=\:\frac{\mathrm{logplogp}^{\mathrm{2}} }{\mathrm{logrlogq}} \\ $$$$=\:\frac{\mathrm{logp}}{\mathrm{logr}}\:×\:\frac{\mathrm{logp}^{\mathrm{2}} }{\mathrm{logq}} \\ $$$$=\:\mathrm{log}_{\mathrm{r}} \mathrm{p}\:×\:\mathrm{2log}_{\mathrm{q}} \mathrm{p} \\ $$$$=\:\mathrm{2log}_{\mathrm{q}} \mathrm{plog}_{\mathrm{r}} \mathrm{p} \\ $$$$\mathrm{QED} \\ $$
