
Previous in Differential Equation Next in Differential Equation
Question Number 17735 by tawa tawa last updated on 09/Jul/17
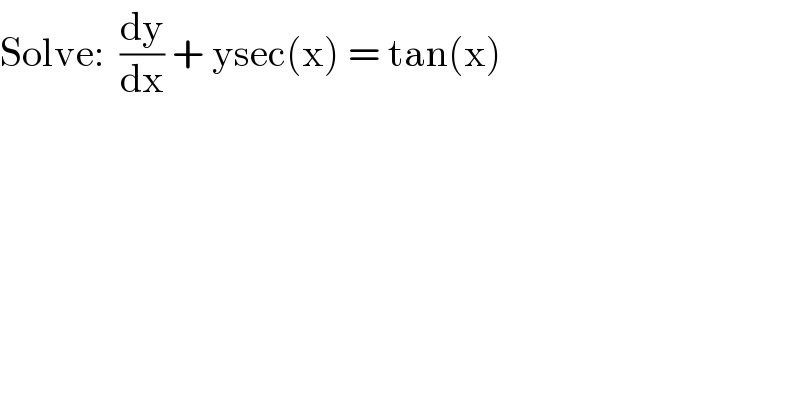
$$\mathrm{Solve}:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\mathrm{ysec}\left(\mathrm{x}\right)\:=\:\mathrm{tan}\left(\mathrm{x}\right) \\ $$
Answered by alex041103 last updated on 10/Jul/17
![So let′s find function μ(x) wich satisfies the followinv (dy/dx)μ+P(x)μy=(d/dx)[yμ] We know that (d/dx)[yμ]=(dy/dx)μ+y(dμ/dx) ⇒P(x)μ=(dμ/dx) Now solving the saparable differential equation P(x) dx = (1/μ) dμ ⇒∫P(x) dx = ∫(1/μ) dμ or ln∣μ∣=∫P(x) dx (we won′t worry about the constant) ⇒μ(x)=e^(∫P(x) dx) Now we apply the μ(x) to solve the differential equation we started with. P(x)=sec x ⇒μ(x)=e^(∫sec x dx) We know the trivial result ∫sec x dx =ln∣sec x + tan x∣ (+C) ⇒μ(x)=sec x + tan x ⇒tan x(sec x + tan x)=(d/dx)[y(sec x + tan x)] ⇒y(x) = ((∫tan x sec x dx + ∫tan^2 x dx)/(sec x + tan x)) We solve the integrals an we get y(x) = 1− ((x + C)/(sec x + tan x))](Q17785.png)
$$\mathrm{So}\:\mathrm{let}'\mathrm{s}\:\mathrm{find}\:\mathrm{function}\:\mu\left(\mathrm{x}\right)\:\mathrm{wich}\:\mathrm{satisfies}\:\mathrm{the}\:\mathrm{followinv} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\mu+\mathrm{P}\left(\mathrm{x}\right)\mu\mathrm{y}=\frac{\mathrm{d}}{\mathrm{dx}}\left[\mathrm{y}\mu\right] \\ $$$$\mathrm{We}\:\mathrm{know}\:\mathrm{that} \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left[\mathrm{y}\mu\right]=\frac{\mathrm{dy}}{\mathrm{dx}}\mu+\mathrm{y}\frac{\mathrm{d}\mu}{\mathrm{dx}} \\ $$$$\Rightarrow\mathrm{P}\left(\mathrm{x}\right)\mu=\frac{\mathrm{d}\mu}{\mathrm{dx}} \\ $$$$\mathrm{Now}\:\mathrm{solving}\:\mathrm{the}\:\mathrm{saparable}\:\mathrm{differential} \\ $$$$\mathrm{equation} \\ $$$$\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mu}\:\mathrm{d}\mu \\ $$$$\Rightarrow\int\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{dx}\:=\:\int\frac{\mathrm{1}}{\mu}\:\mathrm{d}\mu \\ $$$$\mathrm{or}\:\mathrm{ln}\mid\mu\mid=\int\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{dx}\:\left(\mathrm{we}\:\mathrm{won}'\mathrm{t}\:\mathrm{worry}\:\mathrm{about}\:\mathrm{the}\:\mathrm{constant}\right) \\ $$$$\Rightarrow\mu\left(\mathrm{x}\right)=\mathrm{e}^{\int\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{dx}} \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{apply}\:\mathrm{the}\:\mu\left(\mathrm{x}\right)\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{differential} \\ $$$$\mathrm{equation}\:\mathrm{we}\:\mathrm{started}\:\mathrm{with}. \\ $$$$\mathrm{P}\left(\mathrm{x}\right)=\mathrm{sec}\:\mathrm{x} \\ $$$$\Rightarrow\mu\left(\mathrm{x}\right)=\mathrm{e}^{\int\mathrm{sec}\:\mathrm{x}\:\mathrm{dx}} \\ $$$$\mathrm{We}\:\mathrm{know}\:\mathrm{the}\:\mathrm{trivial}\:\mathrm{result}\:\int\mathrm{sec}\:\mathrm{x}\:\mathrm{dx} \\ $$$$=\mathrm{ln}\mid\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}\mid\:\left(+\mathrm{C}\right) \\ $$$$\Rightarrow\mu\left(\mathrm{x}\right)=\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{x}\left(\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}\right)=\frac{\mathrm{d}}{\mathrm{dx}}\left[\mathrm{y}\left(\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}\right)\right] \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\:\frac{\int\mathrm{tan}\:\mathrm{x}\:\mathrm{sec}\:\mathrm{x}\:\mathrm{dx}\:+\:\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}}{\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}} \\ $$$$\mathrm{We}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{integrals}\:\mathrm{an}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\:\mathrm{1}−\:\frac{\mathrm{x}\:+\:\mathrm{C}}{\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}} \\ $$$$ \\ $$
Commented by alex041103 last updated on 10/Jul/17
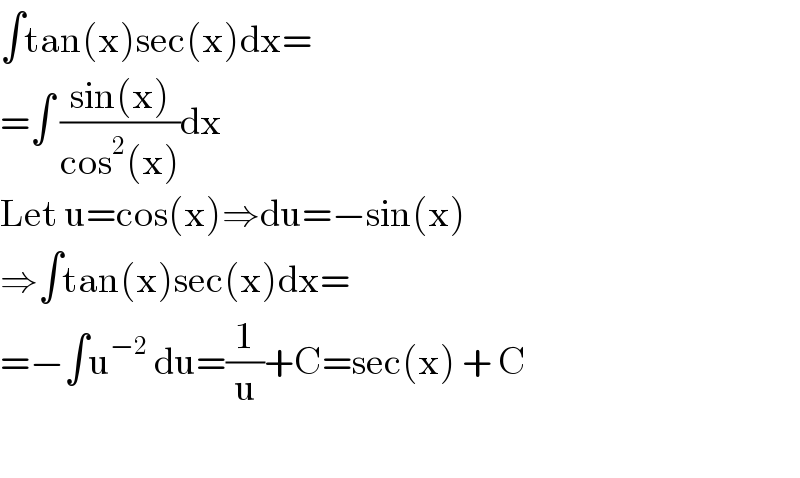
$$\int\mathrm{tan}\left(\mathrm{x}\right)\mathrm{sec}\left(\mathrm{x}\right)\mathrm{dx}= \\ $$$$=\int\:\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$\mathrm{Let}\:\mathrm{u}=\mathrm{cos}\left(\mathrm{x}\right)\Rightarrow\mathrm{du}=−\mathrm{sin}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\int\mathrm{tan}\left(\mathrm{x}\right)\mathrm{sec}\left(\mathrm{x}\right)\mathrm{dx}= \\ $$$$=−\int\mathrm{u}^{−\mathrm{2}} \:\mathrm{du}=\frac{\mathrm{1}}{\mathrm{u}}+\mathrm{C}=\mathrm{sec}\left(\mathrm{x}\right)\:+\:\mathrm{C} \\ $$$$ \\ $$
Commented by tawa tawa last updated on 10/Jul/17
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by alex041103 last updated on 10/Jul/17
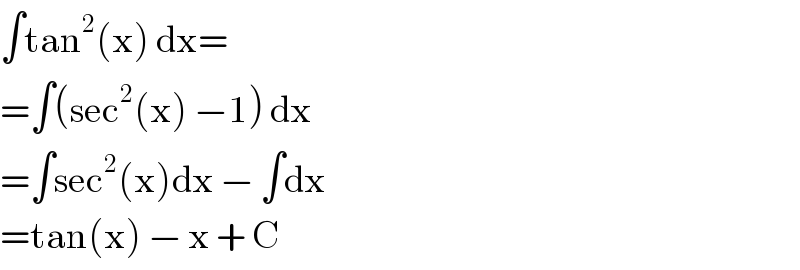
$$\int\mathrm{tan}^{\mathrm{2}} \left(\mathrm{x}\right)\:\mathrm{dx}= \\ $$$$=\int\left(\mathrm{sec}^{\mathrm{2}} \left(\mathrm{x}\right)\:−\mathrm{1}\right)\:\mathrm{dx} \\ $$$$=\int\mathrm{sec}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx}\:−\:\int\mathrm{dx} \\ $$$$=\mathrm{tan}\left(\mathrm{x}\right)\:−\:\mathrm{x}\:+\:\mathrm{C} \\ $$
