Question Number 17729 by Tinkutara last updated on 09/Jul/17

$$\mathrm{A}\:\mathrm{lotus}\:\mathrm{plant}\:\mathrm{in}\:\mathrm{a}\:\mathrm{pool}\:\mathrm{of}\:\mathrm{water}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cubit}\:\mathrm{above}\:\mathrm{water}\:\mathrm{level}.\:\mathrm{When} \\ $$$$\mathrm{propelled}\:\mathrm{by}\:\mathrm{air},\:\mathrm{the}\:\mathrm{lotus}\:\mathrm{sinks}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{pool}\:\mathrm{2}\:\mathrm{cubits}\:\mathrm{away}\:\mathrm{from}\:\mathrm{its}\:\mathrm{position}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{depth}\:\mathrm{of}\:\mathrm{water}\:\mathrm{in}\:\mathrm{the}\:\mathrm{pool}. \\ $$
Commented by alex041103 last updated on 10/Jul/17
$$\mathrm{What}\:\mathrm{does}\:\mathrm{a}\:'\mathrm{cubit}'\mathrm{mean}?\mathrm{I}'\mathrm{m}\:\mathrm{sorry}\:\mathrm{for}\:\mathrm{my}\:\mathrm{english}. \\ $$
Commented by mrW1 last updated on 10/Jul/17
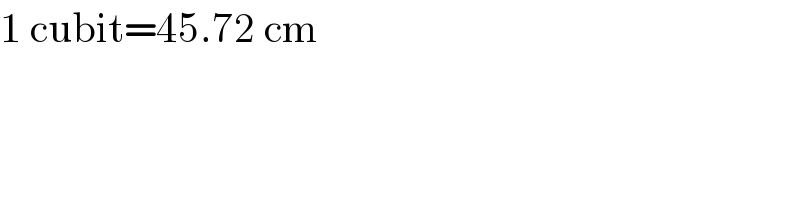
$$\mathrm{1}\:\mathrm{cubit}=\mathrm{45}.\mathrm{72}\:\mathrm{cm} \\ $$
Commented by mrW1 last updated on 10/Jul/17
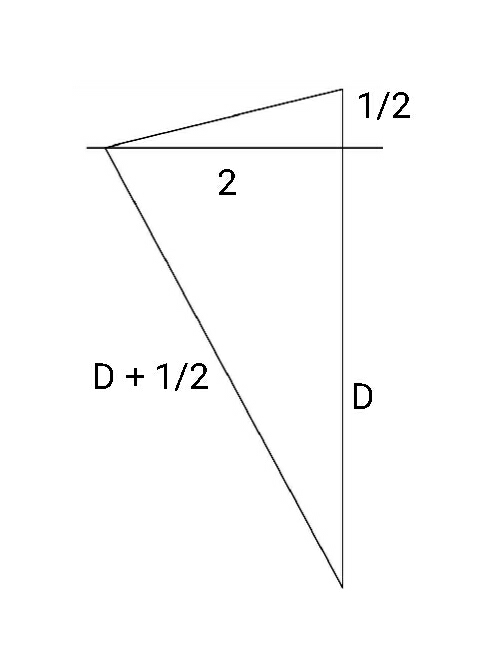
Answered by mrW1 last updated on 10/Jul/17
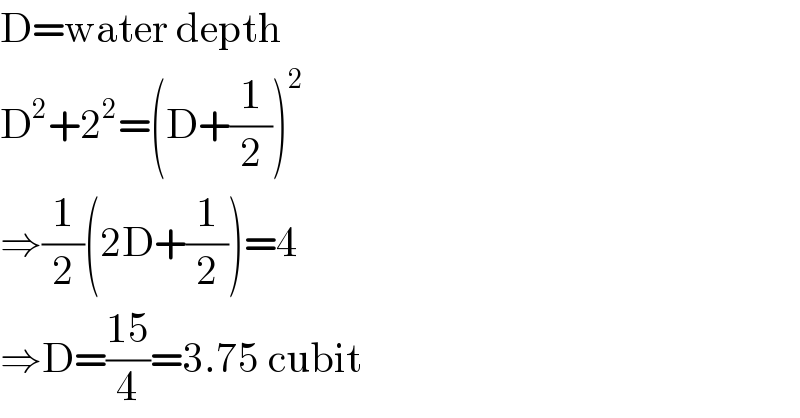
$$\mathrm{D}=\mathrm{water}\:\mathrm{depth} \\ $$$$\mathrm{D}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} =\left(\mathrm{D}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2D}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{4} \\ $$$$\Rightarrow\mathrm{D}=\frac{\mathrm{15}}{\mathrm{4}}=\mathrm{3}.\mathrm{75}\:\mathrm{cubit} \\ $$
Commented by Tinkutara last updated on 11/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Commented by ajfour last updated on 11/Jul/17
$$\mathrm{couldn}'\mathrm{t}\:\mathrm{follow}\:\mathrm{the}\:\mathrm{geometry}.. \\ $$
Commented by Tinkutara last updated on 11/Jul/17