Question and Answers Forum

All Question   Topic List

Question Number 177253 by BaliramKumar last updated on 02/Oct/22

$$ \\ $$ The base of a right pyramid is a hexagon of side 16 cm, and its lateral surface is 720 sq. cm. Is. the height of the pyramid will be\\n

Answered by HeferH last updated on 02/Oct/22

(√(33 )) ?

$$\sqrt{\mathrm{33}\:}\:?\: \\ $$

Answered by a.lgnaoui last updated on 02/Oct/22

soit AB base du pyramide hexagonsle hauteur du pyramide OA rayon du ceecle circonscrit syrfsce de la base est ((AB×CD)/2) Surface laterale S=6×((AB×CD)/2)=3AB×CD CD=(S/(3AB))=((720)/(48))=15 CD^2 =OC^2 +x^2 (x=haureur) OC=OAsin 60=16×((√3)/2)=8(√3) x^2 =CD^2 −OC^2 =225−192=33 x=(√(33)) =5,74cm

$${soit}\:\mathrm{AB}\:\mathrm{base}\:\mathrm{du}\:\mathrm{pyramide}\:\mathrm{hexagonsle} \\ $$ $$\:\:\:\:\:\:\:\mathrm{hauteur}\:\mathrm{du}\:\mathrm{pyramide} \\ $$ $$\mathrm{OA}\:\:\mathrm{rayon}\:\mathrm{du}\:\mathrm{ceecle}\:\mathrm{circonscrit} \\ $$ $$\mathrm{syrfsce}\:\mathrm{de}\:\mathrm{la}\:\mathrm{base}\:\mathrm{est}\:\frac{\mathrm{AB}×\mathrm{CD}}{\mathrm{2}}\:\:\:\: \\ $$ $$\mathrm{Surface}\:\mathrm{laterale}\:\:\mathrm{S}=\mathrm{6}×\frac{\mathrm{AB}×\mathrm{CD}}{\mathrm{2}}=\mathrm{3AB}×\mathrm{CD} \\ $$ $$\mathrm{CD}=\frac{\mathrm{S}}{\mathrm{3AB}}=\frac{\mathrm{720}}{\mathrm{48}}=\mathrm{15} \\ $$ $$\mathrm{CD}^{\mathrm{2}} =\mathrm{OC}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \:\:\:\:\left(\mathrm{x}=\mathrm{haureur}\right) \\ $$ $$\mathrm{OC}=\mathrm{OAsin}\:\mathrm{60}=\mathrm{16}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{8}\sqrt{\mathrm{3}} \\ $$ $$\mathrm{x}^{\mathrm{2}} =\mathrm{CD}^{\mathrm{2}} −\mathrm{OC}^{\mathrm{2}} =\mathrm{225}−\mathrm{192}=\mathrm{33} \\ $$ $$\mathrm{x}=\sqrt{\mathrm{33}}\:=\mathrm{5},\mathrm{74}{cm} \\ $$

Commented bya.lgnaoui last updated on 02/Oct/22

Commented bya.lgnaoui last updated on 02/Oct/22

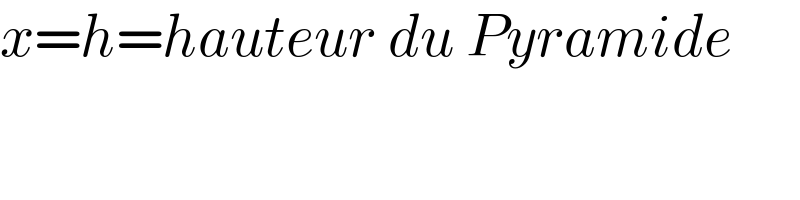
x=h=hauteur du Pyramide

$${x}={h}={hauteur}\:{du}\:{Pyramide} \\ $$

Commented byBaliramKumar last updated on 03/Oct/22

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com