
Question Number 177173 by Shrinava last updated on 01/Oct/22
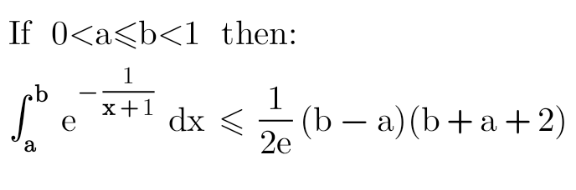
Answered by Peace last updated on 02/Oct/22
![let f(x)=e^(−(1/(x+1))) ,applie Taylors lagrange formul ⇒∃c∈[0,1] such that f(x)=f(0)+xf′(c)=e^(−1) +x.(e^(−(1/(1+c))) /((1+c)^2 )) We have ∀c∈[0,1] (e^(−(1/(1+c))) /((1+c)^2 ))≤1⇔t^2 e^(−t) ≤e^(−1) ,∀t∈[(1/2),1] Wich is True (e^t /t^2 )=g(t),g′(t)=((t(t−2)e^t )/t^4 )<0,∀t∈[(1/2),1] g(t)≥g(1)=e⇒et^2 ≥e^t ⇔t^2 e^(−t) ≤e^(−1) ⇒ ⇒f(x)≤e^(−1) +xe^(−1) ∫_a ^b f(x)dx≤e^(−1) ∫_a ^b (1+x)dx=e^(−1) (b−a+((b^2 −a^2 )/2))=(((b−a))/(2e))(2+b+a)](Q177246.png)
$${let}\:{f}\left({x}\right)={e}^{−\frac{\mathrm{1}}{{x}+\mathrm{1}}} ,{applie}\:{Taylors}\:{lagrange}\:{formul}\:\Rightarrow\exists{c}\in\left[\mathrm{0},\mathrm{1}\right]\:{such}\:{that} \\ $$$${f}\left({x}\right)={f}\left(\mathrm{0}\right)+{xf}'\left({c}\right)={e}^{−\mathrm{1}} +{x}.\frac{{e}^{−\frac{\mathrm{1}}{\mathrm{1}+{c}}} }{\left(\mathrm{1}+{c}\right)^{\mathrm{2}} } \\ $$$${We}\:{have}\:\forall{c}\in\left[\mathrm{0},\mathrm{1}\right]\:\frac{{e}^{−\frac{\mathrm{1}}{\mathrm{1}+{c}}} }{\left(\mathrm{1}+{c}\right)^{\mathrm{2}} }\leqslant\mathrm{1}\Leftrightarrow{t}^{\mathrm{2}} {e}^{−{t}} \leqslant{e}^{−\mathrm{1}} ,\forall{t}\in\left[\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}\right] \\ $$$${Wich}\:{is}\:{True}\:\frac{{e}^{{t}} }{{t}^{\mathrm{2}} }={g}\left({t}\right),{g}'\left({t}\right)=\frac{{t}\left({t}−\mathrm{2}\right){e}^{{t}} }{{t}^{\mathrm{4}} }<\mathrm{0},\forall{t}\in\left[\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}\right] \\ $$$${g}\left({t}\right)\geqslant{g}\left(\mathrm{1}\right)={e}\Rightarrow{et}^{\mathrm{2}} \geqslant{e}^{{t}} \Leftrightarrow{t}^{\mathrm{2}} {e}^{−{t}} \leqslant{e}^{−\mathrm{1}} \Rightarrow \\ $$$$\Rightarrow{f}\left({x}\right)\leqslant{e}^{−\mathrm{1}} +{xe}^{−\mathrm{1}} \\ $$$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}\leqslant{e}^{−\mathrm{1}} \int_{{a}} ^{{b}} \left(\mathrm{1}+{x}\right){dx}={e}^{−\mathrm{1}} \left({b}−{a}+\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}}\right)=\frac{\left({b}−{a}\right)}{\mathrm{2}{e}}\left(\mathrm{2}+{b}+{a}\right) \\ $$
