
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 1771 by hareem ali last updated on 19/Sep/15
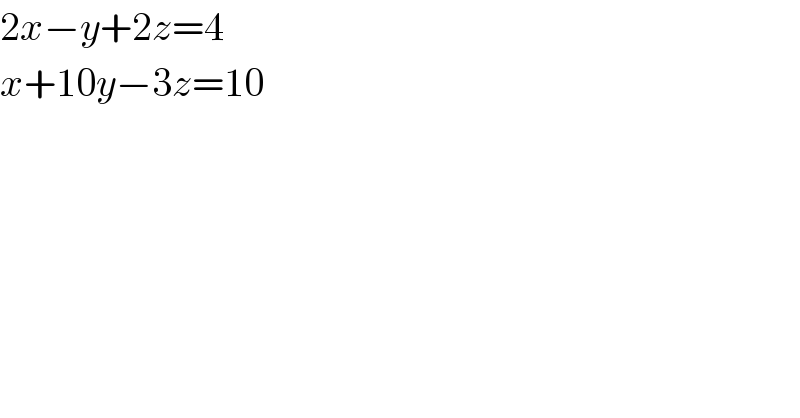
$$\mathrm{2}{x}−{y}+\mathrm{2}{z}=\mathrm{4} \\ $$$${x}+\mathrm{10}{y}−\mathrm{3}{z}=\mathrm{10} \\ $$
Answered by 123456 last updated on 19/Sep/15
![[(2,(−1),2),(1,(10),(−3)),(0,0,0) ] [(x),(y),(z) ]= [(4),((10)),(0) ] [(2,(−1),2,4),(1,(10),(−3),(10)) ] ∼ [(2,(−1),2,4),(2,(20),(−6),(20)) ] ∼ [(2,(−1),2,4),(0,(21),(−8),(16)) ] ∼ [((42),(−21),(42),(84)),(0,(21),(−8),(16)) ] ∼ [((42),0,(34),(100)),(0,(21),(−8),(16)) ] ∼ [(1,0,((17)/(21)),((50)/(21))),(0,1,(−(8/(21))),((16)/(21))) ] [(x),(y),(z) ]= [(((50−17t)/(21))),(((16+8t)/(21))),(t) ]](Q1772.png)
$$\begin{bmatrix}{\mathrm{2}}&{−\mathrm{1}}&{\mathrm{2}}\\{\mathrm{1}}&{\mathrm{10}}&{−\mathrm{3}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}\end{bmatrix}\begin{bmatrix}{{x}}\\{{y}}\\{{z}}\end{bmatrix}=\begin{bmatrix}{\mathrm{4}}\\{\mathrm{10}}\\{\mathrm{0}}\end{bmatrix} \\ $$$$\begin{bmatrix}{\mathrm{2}}&{−\mathrm{1}}&{\mathrm{2}}&{\mathrm{4}}\\{\mathrm{1}}&{\mathrm{10}}&{−\mathrm{3}}&{\mathrm{10}}\end{bmatrix} \\ $$$$\sim\begin{bmatrix}{\mathrm{2}}&{−\mathrm{1}}&{\mathrm{2}}&{\mathrm{4}}\\{\mathrm{2}}&{\mathrm{20}}&{−\mathrm{6}}&{\mathrm{20}}\end{bmatrix} \\ $$$$\sim\begin{bmatrix}{\mathrm{2}}&{−\mathrm{1}}&{\mathrm{2}}&{\mathrm{4}}\\{\mathrm{0}}&{\mathrm{21}}&{−\mathrm{8}}&{\mathrm{16}}\end{bmatrix} \\ $$$$\sim\begin{bmatrix}{\mathrm{42}}&{−\mathrm{21}}&{\mathrm{42}}&{\mathrm{84}}\\{\mathrm{0}}&{\mathrm{21}}&{−\mathrm{8}}&{\mathrm{16}}\end{bmatrix} \\ $$$$\sim\begin{bmatrix}{\mathrm{42}}&{\mathrm{0}}&{\mathrm{34}}&{\mathrm{100}}\\{\mathrm{0}}&{\mathrm{21}}&{−\mathrm{8}}&{\mathrm{16}}\end{bmatrix} \\ $$$$\sim\begin{bmatrix}{\mathrm{1}}&{\mathrm{0}}&{\frac{\mathrm{17}}{\mathrm{21}}}&{\frac{\mathrm{50}}{\mathrm{21}}}\\{\mathrm{0}}&{\mathrm{1}}&{−\frac{\mathrm{8}}{\mathrm{21}}}&{\frac{\mathrm{16}}{\mathrm{21}}}\end{bmatrix} \\ $$$$\begin{bmatrix}{{x}}\\{{y}}\\{{z}}\end{bmatrix}=\begin{bmatrix}{\frac{\mathrm{50}−\mathrm{17}{t}}{\mathrm{21}}}\\{\frac{\mathrm{16}+\mathrm{8}{t}}{\mathrm{21}}}\\{{t}}\end{bmatrix} \\ $$
