
Question Number 177030 by mr W last updated on 01/Oct/22
![if (√(x+(√(x+(√(x+(√(x+(√x)))))))))=2022 find [x]=?](Q177030.png)
$${if}\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}}}=\mathrm{2022} \\ $$$${find}\:\left[{x}\right]=? \\ $$
Answered by TheHoneyCat last updated on 30/Sep/22

$$\mathrm{if}\:{x}\:\mathrm{exists},\:\mathrm{squaring}\:\mathrm{the}\:\mathrm{equlity}\:\mathrm{implies}\:\mathrm{that}: \\ $$$${x}+\mathrm{2022}=\left(\mathrm{2022}\right)^{\mathrm{2}} \\ $$$${ie}\:{x}=\mathrm{2022}×\mathrm{2021} \\ $$$$ \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{just}\:\mathrm{need}\:\mathrm{to}\:\mathrm{proove}\:\mathrm{that}\:{x}\:\mathrm{exists} \\ $$$${ie}\:\mathrm{that}\:\mathrm{their}\:\mathrm{exists}\:\mathrm{a}\:\mathrm{value}\:{x}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{denoting}\:{f}_{{x}} \left({y}\right):=\sqrt{{x}+{y}} \\ $$$$\left({f}_{{x}} ^{\:\circ{n}} \left(\mathrm{0}\right)\right)_{{n}\in\mathbb{N}} \:\mathrm{converges}\:\mathrm{to}\:\mathrm{2022} \\ $$$$ \\ $$$$\mathrm{it}\:\mathrm{turns}\:\mathrm{out}\:\mathrm{that}\:\mathrm{if}\:{x}>\mathrm{4}\: \\ $$$$\mathrm{then}\:\sqrt{{x}}<{x}/\mathrm{2}\:\mathrm{and}\:\sqrt{{x}}>\mathrm{2} \\ $$$$\mathrm{so}\:{x}>\mathrm{2}\:\mathrm{and}\:{y}>\mathrm{2}\:\Rightarrow\:\sqrt{{x}+{y}}<\left({x}+{y}\right)/\mathrm{2} \\ $$$$\mathrm{and}\:\mathrm{still}\:\sqrt{{x}+{y}}\:>\mathrm{2} \\ $$$$ \\ $$$$\mathrm{so}\:\mathrm{if}\:{x}>\mathrm{4} \\ $$$$\left(\mathrm{so}\:\mathrm{that}\:\mathrm{the}\:\mathrm{second}\:\mathrm{term}\:\mathrm{is}\:\mathrm{superior}\:\mathrm{to}\:\mathrm{2}\right) \\ $$$$\mathrm{the}\:\mathrm{sequence}\:\mathrm{is}\:\mathrm{always}\:\mathrm{over}\:\mathrm{2}\:\mathrm{and}\:\mathrm{always} \\ $$$$\mathrm{under}\:{U}_{{n}+\mathrm{1}} =\frac{{x}+{U}_{{n}} }{\mathrm{2}}\:\left(\mathrm{with}\:{U}_{\mathrm{1}} ={x}\right) \\ $$$$ \\ $$$$\mathrm{basically}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{is}\:\mathrm{bounded} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{trivial}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{monotonous},\:\mathrm{so} \\ $$$$\mathrm{it}\:\mathrm{converges}. \\ $$$$\mathrm{Denoting}\:\mathrm{by}\:{f}_{\infty} \:\mathrm{its}\:\mathrm{limit} \\ $$$${x}+{f}_{\infty} ={f}_{\infty} ^{\:\mathrm{2}} \\ $$$$\mathrm{which}\:\mathrm{admits}\:\mathrm{solutions}\:\mathrm{for}\:\mathrm{any}\:\mathrm{values}. \\ $$$$\mathrm{including}\:{f}_{\infty} =\mathrm{2022}\:_{\blacksquare} \\ $$$$ \\ $$$$ \\ $$$${Note}\:{that}\:{I}\:{have}\:{assumed}\:{that} \\ $$$$\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+{x}}}}}\:{meant}\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}} \\ $$$$ \\ $$$${if}\:{you}\:{actually}\:{did}\:{meant}\:{your}\:{question} \\ $$$${to}\:{be}\:{about}\:{a}\:{finite}\:{amount}\:{of}\: \\ $$$${square}\:{roots},\:{it}\:{is}\:{equivalent}\:{to}\:{solving} \\ $$$${an}\:{equation}\:{of}\:{degree}\:\mathrm{8}. \\ $$$${Wich}\:\left({in}\:{general}\:{is}\:{not}\:{solvable}\right) \\ $$$${The}\:{polynomial}\:{is}\:{not}\:{symetric}\:\left({so}\:{you}\right. \\ $$$$\left.{cannot}\:{reduce}\:{it}\:{to}\:{deg}=\mathrm{4}\right) \\ $$$${the}\:{coeficients}\:{are}\:{either}\:{divisible}\:{by}\:\mathrm{2022} \\ $$$$\left({that}\:{gives}\:{the}\:{hope}\:{of}\:{looking}\:{for}\:{integer}\right. \\ $$$$\left.{sokutions}\:{throught}\:{congruences}\right)\:{or}\:\pm\mathrm{1}\: \\ $$$$\left({so}\:{I}\:{guess}\:{congruences}\:{are}\:{not}\:{an}\:{option}\right). \\ $$$${Your}\:{polynomial}\:{can}\:{be}\:{constructed} \\ $$$${recursively}\:{by}\:{composition}\:\left({it}'{s}\:{like}\:{the}\right. \\ $$$$\left.{inverse}\:{of}\:{my}\:``{f}^{\:\circ{n}} ''\right)\:{so}\:{I}'{ve}\:{tried}\:{solving} \\ $$$${the}\:{smallers}\:{n}\:{values}\:{in}\:{the}\:{search}\:{of}\:{a}\: \\ $$$${patern}\:{to}\:{use}\:{recursively}.\:{But}\:{found}\:{none}. \\ $$$$ \\ $$$${I}\:{fear}\:{that}\:{the}\:{precise}\:{question}\:{you}\:{have}\: \\ $$$${asked}\:{has}\:{no}\:{explicit}\:{answere}. \\ $$$${However},\:{I}\:{might}\:{be}\:{wrong}\:{on}\:{that}. \\ $$$${If}\:{someone}\:{knows}\:{I}'{m}\:{wrong},\:{could}\:{you} \\ $$$${please}\:{comment}\:{the}\:{answere}\:{please}? \\ $$$${Thanks}. \\ $$
Commented by mr W last updated on 01/Oct/22
![thanks sir! the LHS is an expression with exactly 5 square roots, not infinite ones. btw, the question is not to find x, but to find [x]. as you said, it′s not solvable for x, but maybe solvable for [x], the integer part of x.](Q177054.png)
$${thanks}\:{sir}! \\ $$$${the}\:{LHS}\:{is}\:{an}\:{expression}\:{with}\:{exactly} \\ $$$$\mathrm{5}\:{square}\:{roots},\:{not}\:{infinite}\:{ones}. \\ $$$${btw},\:{the}\:{question}\:{is}\:{not}\:{to}\:{find}\:{x},\:{but} \\ $$$${to}\:{find}\:\left[{x}\right].\: \\ $$$${as}\:{you}\:{said},\:{it}'{s}\:{not}\:{solvable}\:{for}\:{x},\: \\ $$$${but}\:{maybe}\:{solvable}\:{for}\:\left[{x}\right],\:{the}\:{integer} \\ $$$${part}\:{of}\:{x}. \\ $$
Commented by Tawa11 last updated on 02/Oct/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by Frix last updated on 30/Sep/22
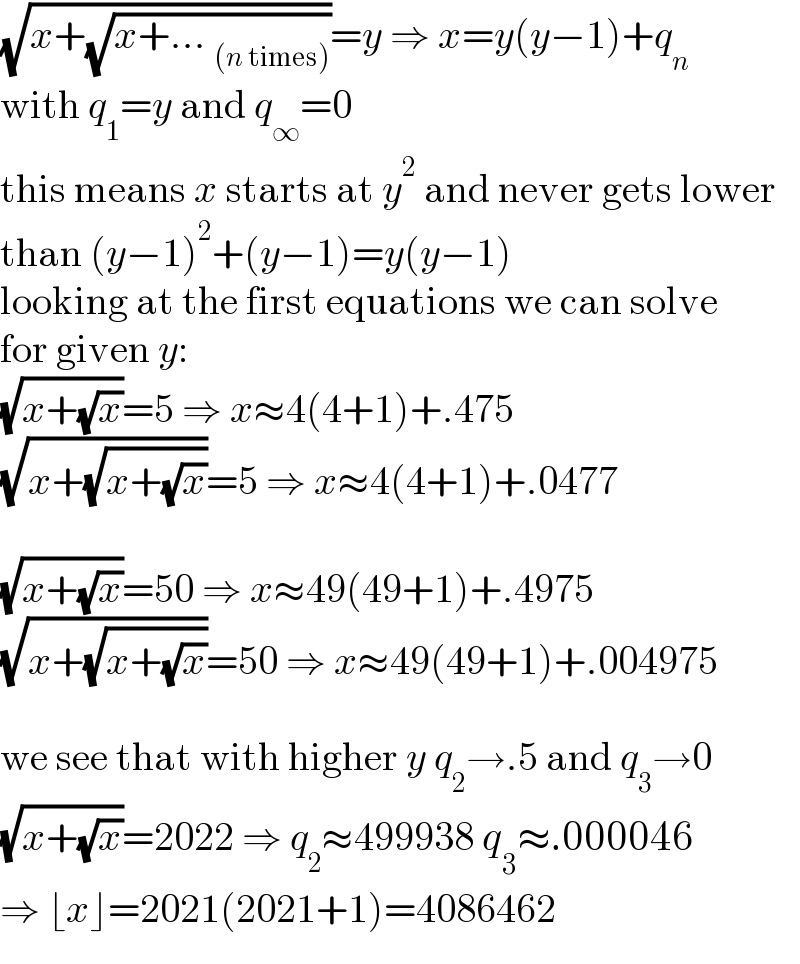
$$\sqrt{{x}+\sqrt{{x}+...\:_{\left({n}\:\mathrm{times}\right)} }}={y}\:\Rightarrow\:{x}={y}\left({y}−\mathrm{1}\right)+{q}_{{n}} \\ $$$$\mathrm{with}\:{q}_{\mathrm{1}} ={y}\:\mathrm{and}\:{q}_{\infty} =\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{means}\:{x}\:\mathrm{starts}\:\mathrm{at}\:{y}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{never}\:\mathrm{gets}\:\mathrm{lower} \\ $$$$\mathrm{than}\:\left({y}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−\mathrm{1}\right)={y}\left({y}−\mathrm{1}\right) \\ $$$$\mathrm{looking}\:\mathrm{at}\:\mathrm{the}\:\mathrm{first}\:\mathrm{equations}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve} \\ $$$$\mathrm{for}\:\mathrm{given}\:{y}: \\ $$$$\sqrt{{x}+\sqrt{{x}}}=\mathrm{5}\:\Rightarrow\:{x}\approx\mathrm{4}\left(\mathrm{4}+\mathrm{1}\right)+.\mathrm{475} \\ $$$$\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}=\mathrm{5}\:\Rightarrow\:{x}\approx\mathrm{4}\left(\mathrm{4}+\mathrm{1}\right)+.\mathrm{0477} \\ $$$$ \\ $$$$\sqrt{{x}+\sqrt{{x}}}=\mathrm{50}\:\Rightarrow\:{x}\approx\mathrm{49}\left(\mathrm{49}+\mathrm{1}\right)+.\mathrm{4975} \\ $$$$\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}=\mathrm{50}\:\Rightarrow\:{x}\approx\mathrm{49}\left(\mathrm{49}+\mathrm{1}\right)+.\mathrm{004975} \\ $$$$ \\ $$$$\mathrm{we}\:\mathrm{see}\:\mathrm{that}\:\mathrm{with}\:\mathrm{higher}\:{y}\:{q}_{\mathrm{2}} \rightarrow.\mathrm{5}\:\mathrm{and}\:{q}_{\mathrm{3}} \rightarrow\mathrm{0} \\ $$$$\sqrt{{x}+\sqrt{{x}}}=\mathrm{2022}\:\Rightarrow\:{q}_{\mathrm{2}} \approx\mathrm{499938}\:{q}_{\mathrm{3}} \approx.\mathrm{000046} \\ $$$$\Rightarrow\:\lfloor{x}\rfloor=\mathrm{2021}\left(\mathrm{2021}+\mathrm{1}\right)=\mathrm{4086462} \\ $$
Commented by mr W last updated on 30/Sep/22
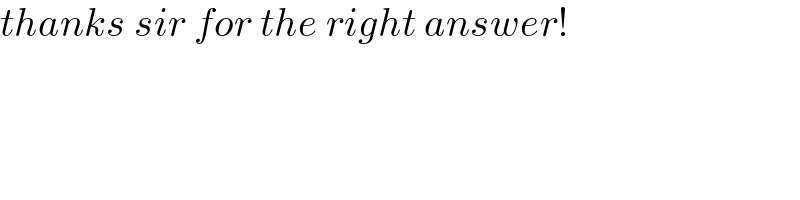
$${thanks}\:{sir}\:{for}\:{the}\:{right}\:{answer}! \\ $$
Answered by mr W last updated on 01/Oct/22
![we have (√(x+(√x)))_(2 times roots) ≤(√(x+(√(x+(√(x+...+(√x)))))))_(n times roots) <(√(x+(√(x+(√(x+(√(x+...))))))))_(infinite times roots) with n∈N and n≥2 if (√(x_2 +(√x_2 )))=2022 and (√(x_n +(√(x_n +(√(x_n +...+(√x_n )))))))=2022 and (√(x_∞ +(√(x_∞ +(√(x_∞ +...))))))=2022 then we have x_∞ <x_n ≤x_2 (√(x_2 +(√x_2 )))=2022 x_2 +(√x_2 )=2022^2 x_2 =(2022^2 −x_2 )^2 x_2 =2022^4 −2×2022^2 x_2 +x_2 ^2 x_2 ^2 −(2×2022^2 +1)x_2 +2022^4 =0 x_2 =((2×2022^2 +1−(√((2×2022^2 +1)^2 −4×2022^4 )))/2) =((2×2022^2 +1−(√(4×2022^2 +1)))/2) <((2×2022^2 +1−(√(4×2022^2 )))/2) =((2×2022^2 +1−2×2022)/2) =2022^2 −2022+(1/2) =2021×2022+(1/2) (√(x_∞ +2022))=2022 ⇒x_∞ =2022^2 −2022=2021×2022 from x_∞ <x_n ≤x_2 we get 2021×2022<x_n <2021×2022+(1/2) that means [x_n ]=2021×2022=4086462 generally if (√(x+(√(x+(√(x+...+(√x)))))))_(2 or more, but finite roots) =k ∈ N ∧ k≥1 then [x]=(k−1)k](Q177104.png)
$${we}\:{have} \\ $$$$\:\underset{\mathrm{2}\:{times}\:{roots}} {\sqrt{{x}+\sqrt{{x}}}}\leqslant\underset{{n}\:{times}\:{roots}} {\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...+\sqrt{{x}}}}}}<\underset{{infinite}\:{times}\:{roots}} {\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}}}} \\ $$$${with}\:{n}\in{N}\:{and}\:{n}\geqslant\mathrm{2} \\ $$$$ \\ $$$${if}\:\sqrt{{x}_{\mathrm{2}} +\sqrt{{x}_{\mathrm{2}} }}=\mathrm{2022} \\ $$$${and}\:\sqrt{{x}_{{n}} +\sqrt{{x}_{{n}} +\sqrt{{x}_{{n}} +...+\sqrt{{x}_{{n}} }}}}=\mathrm{2022} \\ $$$${and}\:\sqrt{{x}_{\infty} +\sqrt{{x}_{\infty} +\sqrt{{x}_{\infty} +...}}}=\mathrm{2022} \\ $$$${then}\:{we}\:{have} \\ $$$${x}_{\infty} <{x}_{{n}} \leqslant{x}_{\mathrm{2}} \\ $$$$ \\ $$$$\sqrt{{x}_{\mathrm{2}} +\sqrt{{x}_{\mathrm{2}} }}=\mathrm{2022} \\ $$$${x}_{\mathrm{2}} +\sqrt{{x}_{\mathrm{2}} }=\mathrm{2022}^{\mathrm{2}} \\ $$$${x}_{\mathrm{2}} =\left(\mathrm{2022}^{\mathrm{2}} −{x}_{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${x}_{\mathrm{2}} =\mathrm{2022}^{\mathrm{4}} −\mathrm{2}×\mathrm{2022}^{\mathrm{2}} {x}_{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${x}_{\mathrm{2}} ^{\mathrm{2}} −\left(\mathrm{2}×\mathrm{2022}^{\mathrm{2}} +\mathrm{1}\right){x}_{\mathrm{2}} +\mathrm{2022}^{\mathrm{4}} =\mathrm{0} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{2}×\mathrm{2022}^{\mathrm{2}} +\mathrm{1}−\sqrt{\left(\mathrm{2}×\mathrm{2022}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{2022}^{\mathrm{4}} }}{\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{2}×\mathrm{2022}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{4}×\mathrm{2022}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}} \\ $$$$\:\:\:\:<\frac{\mathrm{2}×\mathrm{2022}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{4}×\mathrm{2022}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{2}×\mathrm{2022}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}×\mathrm{2022}}{\mathrm{2}} \\ $$$$\:\:\:\:\:=\mathrm{2022}^{\mathrm{2}} −\mathrm{2022}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:=\mathrm{2021}×\mathrm{2022}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\sqrt{{x}_{\infty} +\mathrm{2022}}=\mathrm{2022}\: \\ $$$$\Rightarrow{x}_{\infty} =\mathrm{2022}^{\mathrm{2}} −\mathrm{2022}=\mathrm{2021}×\mathrm{2022} \\ $$$$ \\ $$$${from}\:{x}_{\infty} <{x}_{{n}} \leqslant{x}_{\mathrm{2}} \:{we}\:{get} \\ $$$$\mathrm{2021}×\mathrm{2022}<{x}_{{n}} <\mathrm{2021}×\mathrm{2022}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${that}\:{means}\: \\ $$$$\left[{x}_{{n}} \right]=\mathrm{2021}×\mathrm{2022}=\mathrm{4086462} \\ $$$$ \\ $$$${generally} \\ $$$${if}\:\underset{\mathrm{2}\:{or}\:{more},\:{but}\:{finite}\:{roots}} {\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...+\sqrt{{x}}}}}}={k}\:\in\:{N}\:\wedge\:{k}\geqslant\mathrm{1} \\ $$$${then}\:\left[{x}\right]=\left({k}−\mathrm{1}\right){k} \\ $$
