
Question Number 176915 by thean last updated on 28/Sep/22

Answered by cortano1 last updated on 28/Sep/22
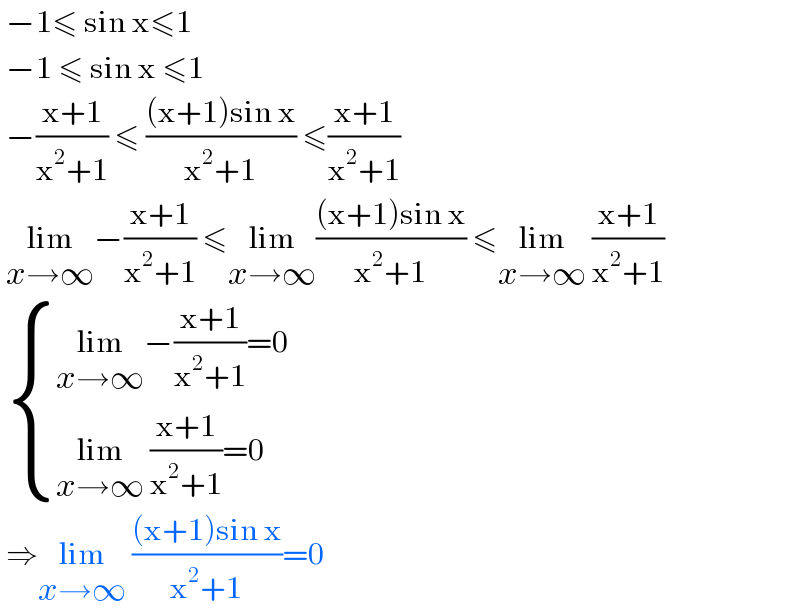
$$\:−\mathrm{1}\leqslant\:\mathrm{sin}\:\mathrm{x}\leqslant\mathrm{1} \\ $$$$\:−\mathrm{1}\:\leqslant\:\mathrm{sin}\:\mathrm{x}\:\leqslant\mathrm{1} \\ $$$$\:−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\leqslant\:\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\leqslant\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\leqslant\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\leqslant\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:\begin{cases}{\underset{{x}\rightarrow\infty} {\mathrm{lim}}−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0}}\\{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0}}\end{cases} \\ $$$$\:\Rightarrow\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$
