
Question Number 176895 by Mastermind last updated on 27/Sep/22
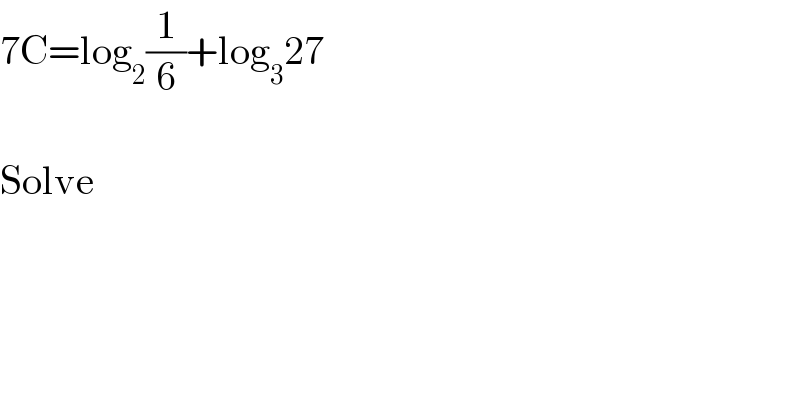
$$\mathrm{7C}=\mathrm{log}_{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{6}}+\mathrm{log}_{\mathrm{3}} \mathrm{27} \\ $$$$ \\ $$$$\mathrm{Solve} \\ $$
Answered by BaliramKumar last updated on 27/Sep/22
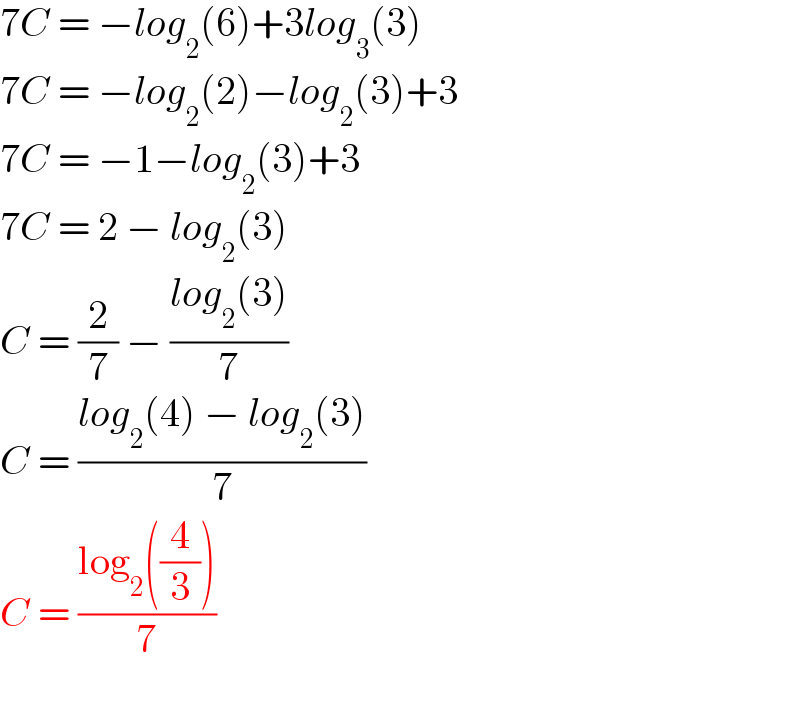
$$\mathrm{7}{C}\:=\:−{log}_{\mathrm{2}} \left(\mathrm{6}\right)+\mathrm{3}{log}_{\mathrm{3}} \left(\mathrm{3}\right) \\ $$$$\mathrm{7}{C}\:=\:−{log}_{\mathrm{2}} \left(\mathrm{2}\right)−{log}_{\mathrm{2}} \left(\mathrm{3}\right)+\mathrm{3} \\ $$$$\mathrm{7}{C}\:=\:−\mathrm{1}−{log}_{\mathrm{2}} \left(\mathrm{3}\right)+\mathrm{3} \\ $$$$\mathrm{7}{C}\:=\:\mathrm{2}\:−\:{log}_{\mathrm{2}} \left(\mathrm{3}\right) \\ $$$${C}\:=\:\frac{\mathrm{2}}{\mathrm{7}}\:−\:\frac{{log}_{\mathrm{2}} \left(\mathrm{3}\right)}{\mathrm{7}} \\ $$$${C}\:=\:\frac{{log}_{\mathrm{2}} \left(\mathrm{4}\right)\:−\:{log}_{\mathrm{2}} \left(\mathrm{3}\right)}{\mathrm{7}} \\ $$$${C}\:=\:\frac{\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)}{\mathrm{7}} \\ $$$$ \\ $$
Answered by Frix last updated on 28/Sep/22
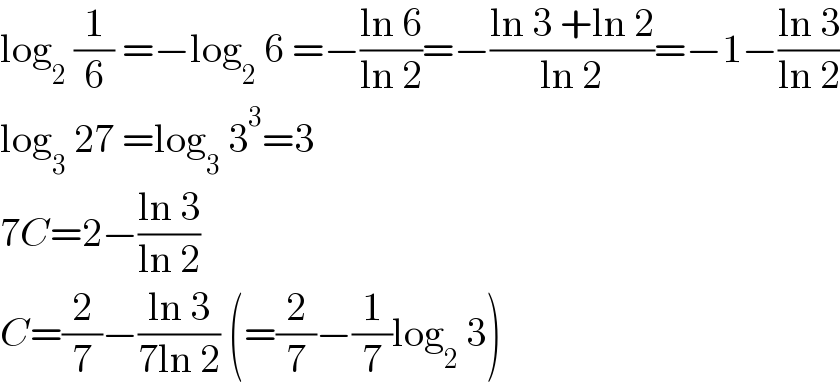
$$\mathrm{log}_{\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{6}}\:=−\mathrm{log}_{\mathrm{2}} \:\mathrm{6}\:=−\frac{\mathrm{ln}\:\mathrm{6}}{\mathrm{ln}\:\mathrm{2}}=−\frac{\mathrm{ln}\:\mathrm{3}\:+\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{2}}=−\mathrm{1}−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}} \\ $$$$\mathrm{log}_{\mathrm{3}} \:\mathrm{27}\:=\mathrm{log}_{\mathrm{3}} \:\mathrm{3}^{\mathrm{3}} =\mathrm{3} \\ $$$$\mathrm{7}{C}=\mathrm{2}−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}} \\ $$$${C}=\frac{\mathrm{2}}{\mathrm{7}}−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{7ln}\:\mathrm{2}}\:\left(=\frac{\mathrm{2}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{7}}\mathrm{log}_{\mathrm{2}} \:\mathrm{3}\right) \\ $$
