
Question Number 176774 by Ar Brandon last updated on 26/Sep/22
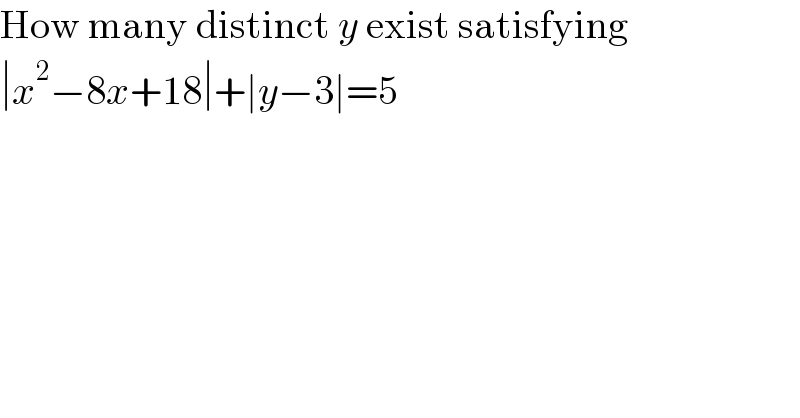
$$\mathrm{How}\:\mathrm{many}\:\mathrm{distinct}\:{y}\:\mathrm{exist}\:\mathrm{satisfying} \\ $$$$\mid{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{18}\mid+\mid{y}−\mathrm{3}\mid=\mathrm{5} \\ $$
Answered by mr W last updated on 26/Sep/22
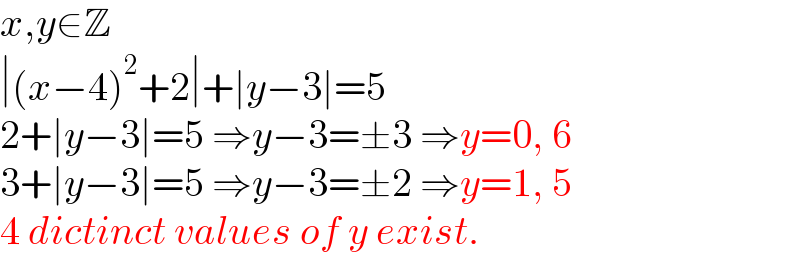
$${x},{y}\in\mathbb{Z} \\ $$$$\mid\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{2}\mid+\mid{y}−\mathrm{3}\mid=\mathrm{5} \\ $$$$\mathrm{2}+\mid{y}−\mathrm{3}\mid=\mathrm{5}\:\Rightarrow{y}−\mathrm{3}=\pm\mathrm{3}\:\Rightarrow{y}=\mathrm{0},\:\mathrm{6} \\ $$$$\mathrm{3}+\mid{y}−\mathrm{3}\mid=\mathrm{5}\:\Rightarrow{y}−\mathrm{3}=\pm\mathrm{2}\:\Rightarrow{y}=\mathrm{1},\:\mathrm{5} \\ $$$$\mathrm{4}\:{dictinct}\:{values}\:{of}\:{y}\:{exist}. \\ $$
Commented by Ar Brandon last updated on 27/Sep/22
Thank you Sir. I now get it.
Commented by mr W last updated on 27/Sep/22
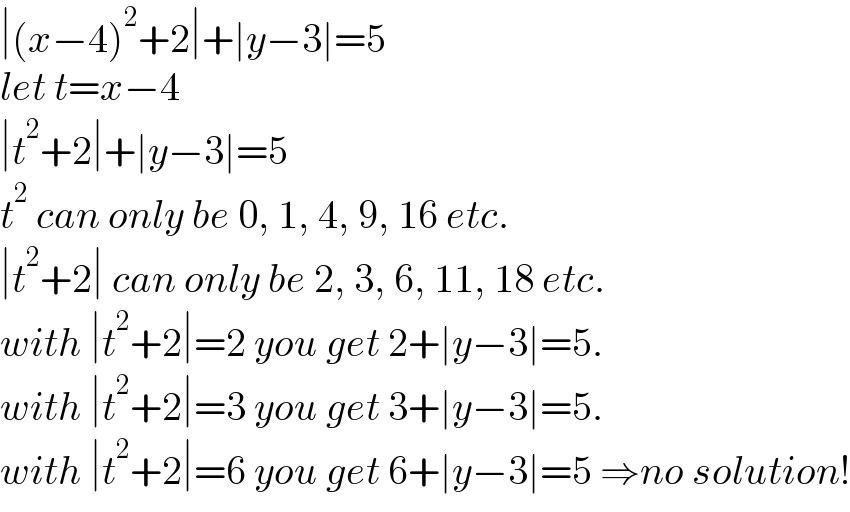
$$\mid\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{2}\mid+\mid{y}−\mathrm{3}\mid=\mathrm{5} \\ $$$${let}\:{t}={x}−\mathrm{4} \\ $$$$\mid{t}^{\mathrm{2}} +\mathrm{2}\mid+\mid{y}−\mathrm{3}\mid=\mathrm{5} \\ $$$${t}^{\mathrm{2}} \:{can}\:{only}\:{be}\:\mathrm{0},\:\mathrm{1},\:\mathrm{4},\:\mathrm{9},\:\mathrm{16}\:{etc}. \\ $$$$\mid{t}^{\mathrm{2}} +\mathrm{2}\mid\:{can}\:{only}\:{be}\:\mathrm{2},\:\mathrm{3},\:\mathrm{6},\:\mathrm{11},\:\mathrm{18}\:{etc}. \\ $$$${with}\:\mid{t}^{\mathrm{2}} +\mathrm{2}\mid=\mathrm{2}\:{you}\:{get}\:\mathrm{2}+\mid{y}−\mathrm{3}\mid=\mathrm{5}. \\ $$$${with}\:\mid{t}^{\mathrm{2}} +\mathrm{2}\mid=\mathrm{3}\:{you}\:{get}\:\mathrm{3}+\mid{y}−\mathrm{3}\mid=\mathrm{5}. \\ $$$${with}\:\mid{t}^{\mathrm{2}} +\mathrm{2}\mid=\mathrm{6}\:{you}\:{get}\:\mathrm{6}+\mid{y}−\mathrm{3}\mid=\mathrm{5}\:\Rightarrow{no}\:{solution}! \\ $$
Commented by Ar Brandon last updated on 26/Sep/22
Great! Thank you, Sir!
Commented by Ar Brandon last updated on 27/Sep/22
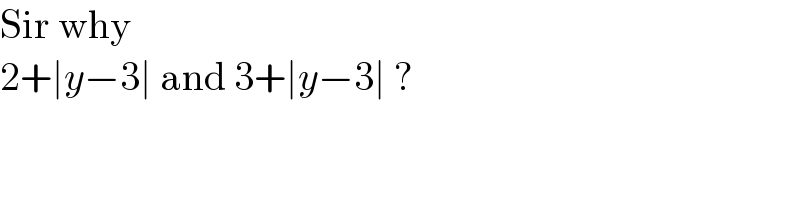
$$\mathrm{Sir}\:\mathrm{why} \\ $$$$\mathrm{2}+\mid{y}−\mathrm{3}\mid\:\mathrm{and}\:\mathrm{3}+\mid{y}−\mathrm{3}\mid\:? \\ $$
