
Question Number 176722 by vishal1234 last updated on 25/Sep/22
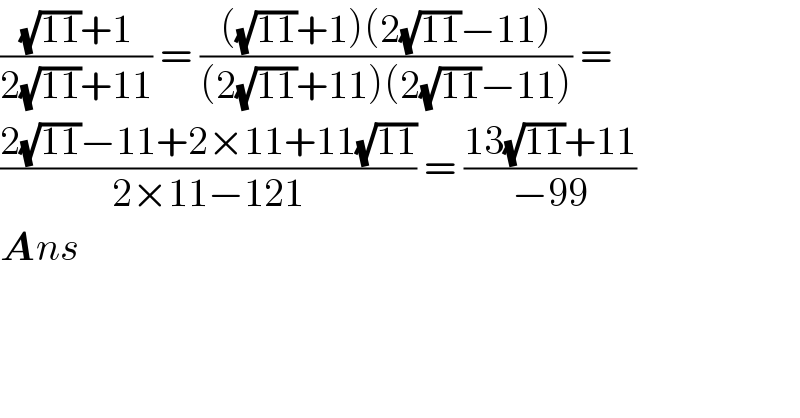
$$\frac{\sqrt{\mathrm{11}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{11}}+\mathrm{11}}\:=\:\frac{\left(\sqrt{\mathrm{11}}+\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{11}}−\mathrm{11}\right)}{\left(\mathrm{2}\sqrt{\mathrm{11}}+\mathrm{11}\right)\left(\mathrm{2}\sqrt{\mathrm{11}}−\mathrm{11}\right)}\:=\: \\ $$$$\frac{\mathrm{2}\sqrt{\mathrm{11}}−\mathrm{11}+\mathrm{2}×\mathrm{11}+\mathrm{11}\sqrt{\mathrm{11}}}{\mathrm{2}×\mathrm{11}−\mathrm{121}}\:=\:\frac{\mathrm{13}\sqrt{\mathrm{11}}+\mathrm{11}}{−\mathrm{99}} \\ $$$$\boldsymbol{{A}}{ns} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Sep/22
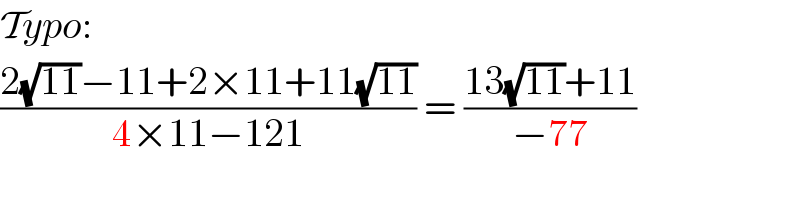
$$\mathcal{T}{ypo}: \\ $$$$\frac{\mathrm{2}\sqrt{\mathrm{11}}−\mathrm{11}+\mathrm{2}×\mathrm{11}+\mathrm{11}\sqrt{\mathrm{11}}}{\mathrm{4}×\mathrm{11}−\mathrm{121}}\:=\:\frac{\mathrm{13}\sqrt{\mathrm{11}}+\mathrm{11}}{−\mathrm{77}} \\ $$
