
Question Number 176662 by Matica last updated on 24/Sep/22
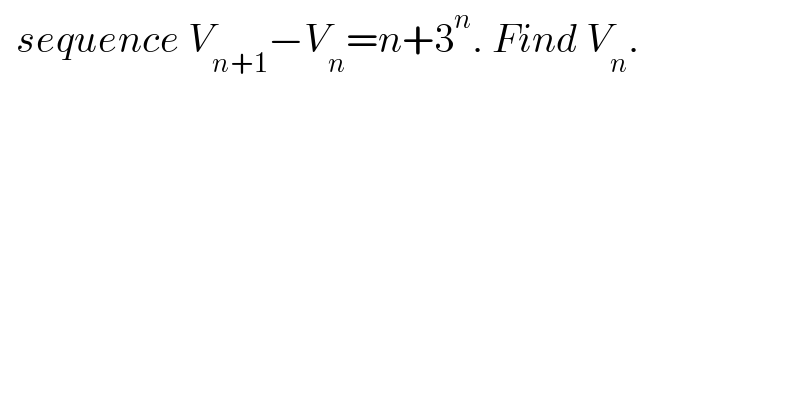
$$\:\:{sequence}\:{V}_{{n}+\mathrm{1}} −{V}_{{n}} ={n}+\mathrm{3}^{{n}} .\:{Find}\:{V}_{{n}} . \\ $$
Answered by mr W last updated on 24/Sep/22
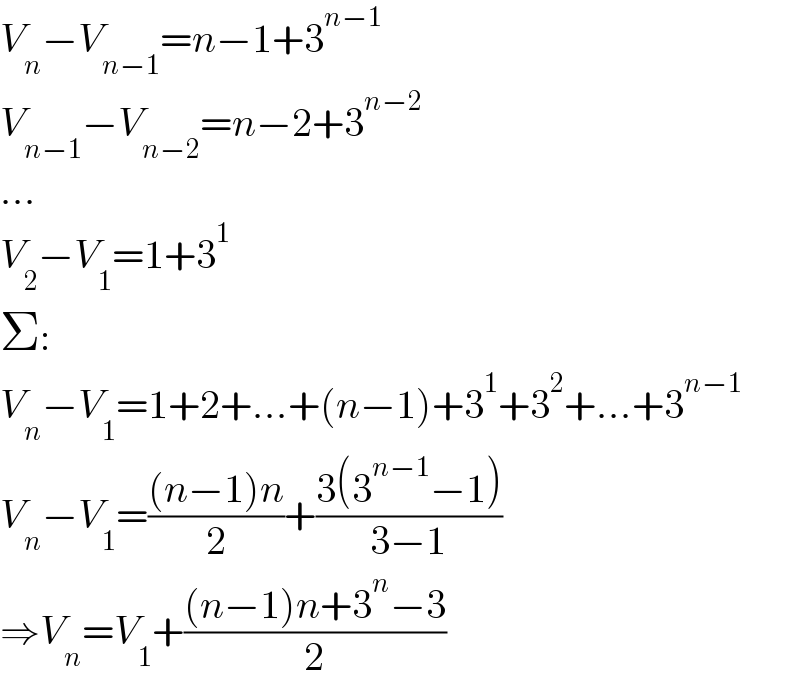
$${V}_{{n}} −{V}_{{n}−\mathrm{1}} ={n}−\mathrm{1}+\mathrm{3}^{{n}−\mathrm{1}} \\ $$$${V}_{{n}−\mathrm{1}} −{V}_{{n}−\mathrm{2}} ={n}−\mathrm{2}+\mathrm{3}^{{n}−\mathrm{2}} \\ $$$$... \\ $$$${V}_{\mathrm{2}} −{V}_{\mathrm{1}} =\mathrm{1}+\mathrm{3}^{\mathrm{1}} \\ $$$$\Sigma: \\ $$$${V}_{{n}} −{V}_{\mathrm{1}} =\mathrm{1}+\mathrm{2}+...+\left({n}−\mathrm{1}\right)+\mathrm{3}^{\mathrm{1}} +\mathrm{3}^{\mathrm{2}} +...+\mathrm{3}^{{n}−\mathrm{1}} \\ $$$${V}_{{n}} −{V}_{\mathrm{1}} =\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}+\frac{\mathrm{3}\left(\mathrm{3}^{{n}−\mathrm{1}} −\mathrm{1}\right)}{\mathrm{3}−\mathrm{1}} \\ $$$$\Rightarrow{V}_{{n}} ={V}_{\mathrm{1}} +\frac{\left({n}−\mathrm{1}\right){n}+\mathrm{3}^{{n}} −\mathrm{3}}{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 25/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mnjuly1970 last updated on 24/Sep/22
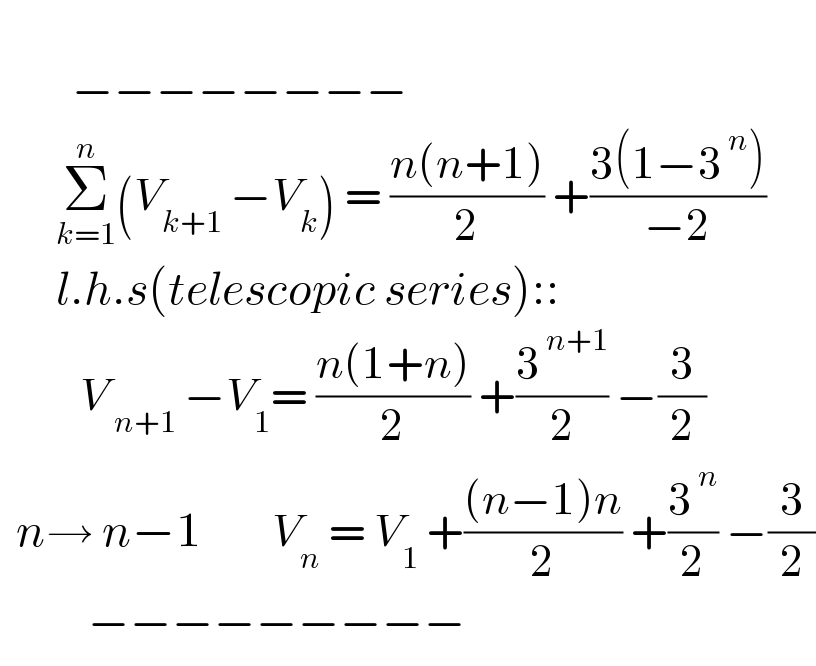
$$\: \\ $$$$\:\:\:\:\:\:\:\:\:−−−−−−−− \\ $$$$\:\:\:\:\:\:\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({V}_{{k}+\mathrm{1}} \:−{V}_{{k}} \right)\:=\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:+\frac{\mathrm{3}\left(\mathrm{1}−\mathrm{3}^{\:{n}} \right)}{−\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:{l}.{h}.{s}\left({telescopic}\:{series}\right):: \\ $$$$\:\:\:\:\:\:\:\:\:\:{V}_{\:{n}+\mathrm{1}} \:−{V}_{\mathrm{1}} =\:\frac{{n}\left(\mathrm{1}+{n}\right)}{\mathrm{2}}\:+\frac{\mathrm{3}^{\:{n}+\mathrm{1}} }{\mathrm{2}}\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:{n}\rightarrow\:{n}−\mathrm{1}\:\:\:\:\:\:\:\:\:{V}_{{n}} \:=\:{V}_{\mathrm{1}} \:+\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}\:+\frac{\mathrm{3}^{\:{n}} }{\mathrm{2}}\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−−−−−−−−− \\ $$
Answered by Mathspace last updated on 25/Sep/22
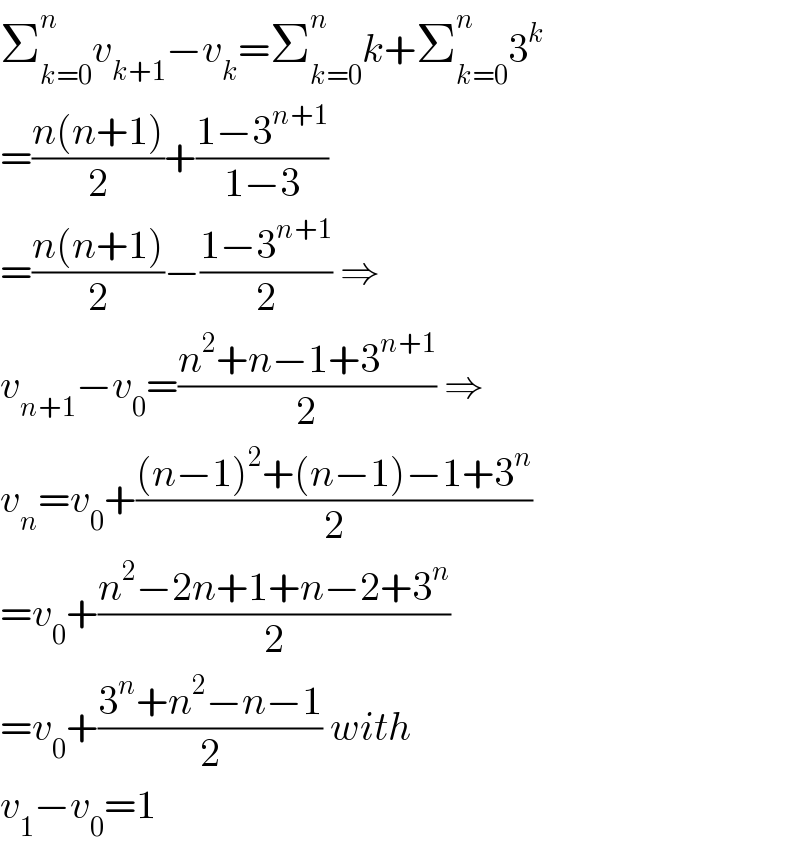
$$\sum_{{k}=\mathrm{0}} ^{{n}} {v}_{{k}+\mathrm{1}} −{v}_{{k}} =\sum_{{k}=\mathrm{0}} ^{{n}} {k}+\sum_{{k}=\mathrm{0}} ^{{n}} \mathrm{3}^{{k}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}+\frac{\mathrm{1}−\mathrm{3}^{{n}+\mathrm{1}} }{\mathrm{1}−\mathrm{3}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}−\frac{\mathrm{1}−\mathrm{3}^{{n}+\mathrm{1}} }{\mathrm{2}}\:\Rightarrow \\ $$$${v}_{{n}+\mathrm{1}} −{v}_{\mathrm{0}} =\frac{{n}^{\mathrm{2}} +{n}−\mathrm{1}+\mathrm{3}^{{n}+\mathrm{1}} }{\mathrm{2}}\:\Rightarrow \\ $$$${v}_{{n}} ={v}_{\mathrm{0}} +\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} +\left({n}−\mathrm{1}\right)−\mathrm{1}+\mathrm{3}^{{n}} }{\mathrm{2}} \\ $$$$={v}_{\mathrm{0}} +\frac{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}+{n}−\mathrm{2}+\mathrm{3}^{{n}} }{\mathrm{2}} \\ $$$$={v}_{\mathrm{0}} +\frac{\mathrm{3}^{{n}} +{n}^{\mathrm{2}} −{n}−\mathrm{1}}{\mathrm{2}}\:{with} \\ $$$${v}_{\mathrm{1}} −{v}_{\mathrm{0}} =\mathrm{1} \\ $$
