
Question Number 176607 by MASANJAJJ last updated on 23/Sep/22
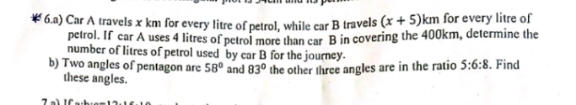
Answered by FelipeLz last updated on 23/Sep/22
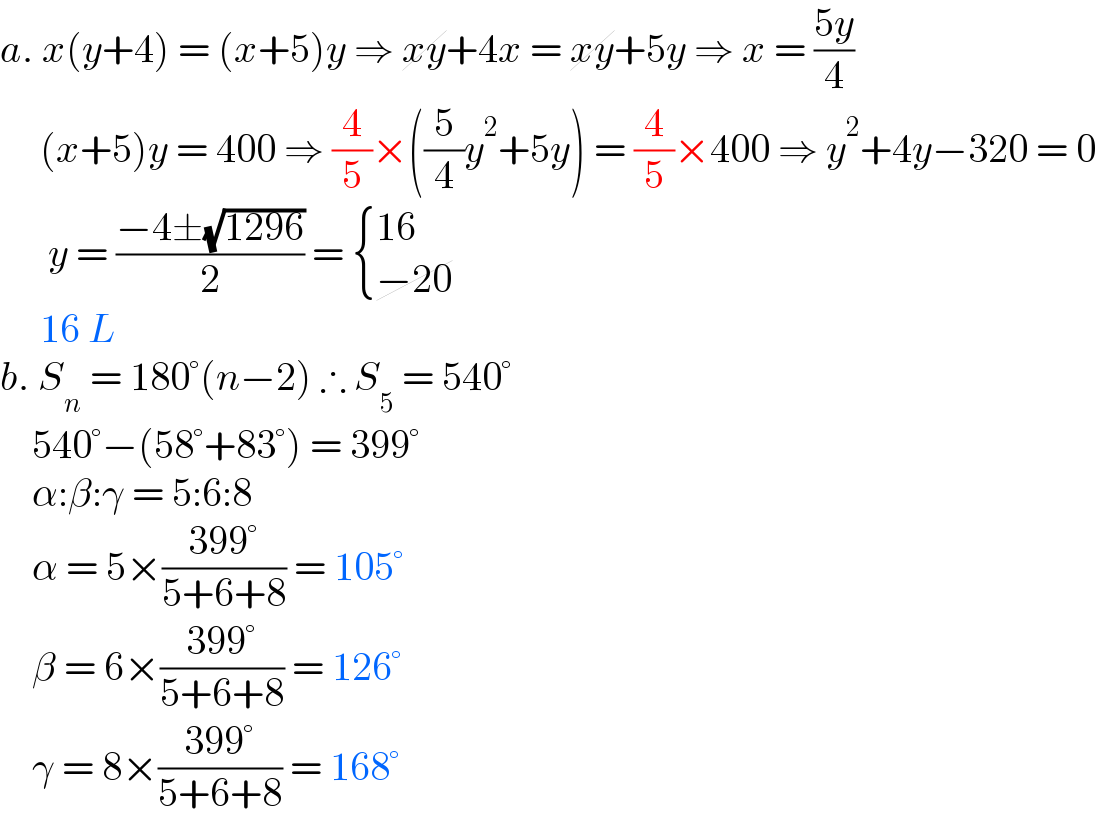
$${a}.\:{x}\left({y}+\mathrm{4}\right)\:=\:\left({x}+\mathrm{5}\right){y}\:\Rightarrow\:\cancel{{xy}}+\mathrm{4}{x}\:=\:\cancel{{xy}}+\mathrm{5}{y}\:\Rightarrow\:{x}\:=\:\frac{\mathrm{5}{y}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\left({x}+\mathrm{5}\right){y}\:=\:\mathrm{400}\:\Rightarrow\:\frac{\mathrm{4}}{\mathrm{5}}×\left(\frac{\mathrm{5}}{\mathrm{4}}{y}^{\mathrm{2}} +\mathrm{5}{y}\right)\:=\:\frac{\mathrm{4}}{\mathrm{5}}×\mathrm{400}\:\Rightarrow\:{y}^{\mathrm{2}} +\mathrm{4}{y}−\mathrm{320}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:{y}\:=\:\frac{−\mathrm{4}\pm\sqrt{\mathrm{1296}}}{\mathrm{2}}\:=\:\begin{cases}{\mathrm{16}\:}\\{\cancel{−\mathrm{20}}}\end{cases} \\ $$$$\:\:\:\:\:\mathrm{16}\:{L} \\ $$$${b}.\:{S}_{{n}} \:=\:\mathrm{180}°\left({n}−\mathrm{2}\right)\:\therefore\:{S}_{\mathrm{5}} \:=\:\mathrm{540}° \\ $$$$\:\:\:\:\mathrm{540}°−\left(\mathrm{58}°+\mathrm{83}°\right)\:=\:\mathrm{399}° \\ $$$$\:\:\:\:\alpha:\beta:\gamma\:=\:\mathrm{5}:\mathrm{6}:\mathrm{8} \\ $$$$\:\:\:\:\alpha\:=\:\mathrm{5}×\frac{\mathrm{399}°}{\mathrm{5}+\mathrm{6}+\mathrm{8}}\:=\:\mathrm{105}° \\ $$$$\:\:\:\:\beta\:=\:\mathrm{6}×\frac{\mathrm{399}°}{\mathrm{5}+\mathrm{6}+\mathrm{8}}\:=\:\mathrm{126}° \\ $$$$\:\:\:\:\gamma\:=\:\mathrm{8}×\frac{\mathrm{399}°}{\mathrm{5}+\mathrm{6}+\mathrm{8}}\:=\:\mathrm{168}° \\ $$
Commented by Tawa11 last updated on 23/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
