
Question Number 176589 by Ar Brandon last updated on 22/Sep/22
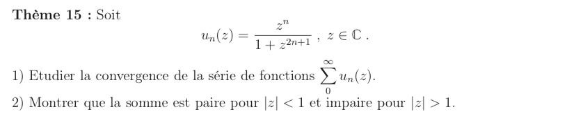
Answered by Peace last updated on 23/Sep/22
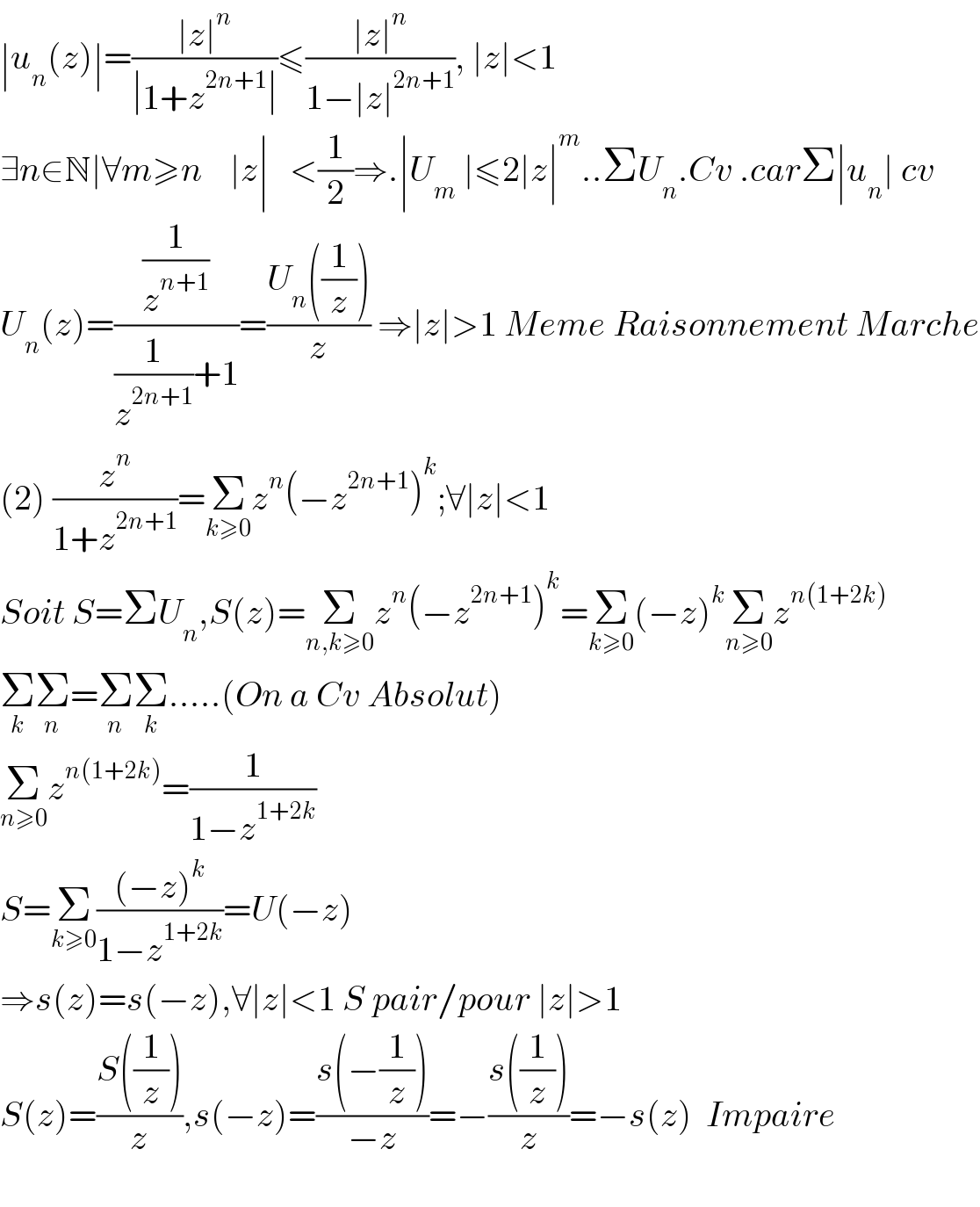
$$\mid{u}_{{n}} \left({z}\right)\mid=\frac{\mid{z}\mid^{{n}} }{\mid\mathrm{1}+{z}^{\mathrm{2}{n}+\mathrm{1}} \mid}\leqslant\frac{\mid{z}\mid^{{n}} }{\mathrm{1}−\mid{z}\mid^{\mathrm{2}{n}+\mathrm{1}} },\:\mid{z}\mid<\mathrm{1} \\ $$$$\exists{n}\in\mathbb{N}\mid\forall{m}\geqslant{n}\:\:\:\:\mid{z}\mid\:\:\:<\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow.\mid{U}_{{m}} \:\mid\leqslant\mathrm{2}\mid{z}\mid^{{m}} ..\Sigma{U}_{{n}} .{Cv}\:.{car}\Sigma\mid{u}_{{n}} \mid\:{cv} \\ $$$${U}_{{n}} \left({z}\right)=\frac{\frac{\mathrm{1}}{{z}^{{n}+\mathrm{1}} }}{\frac{\mathrm{1}}{{z}^{\mathrm{2}{n}+\mathrm{1}} }+\mathrm{1}}=\frac{{U}_{{n}} \left(\frac{\mathrm{1}}{{z}}\right)}{{z}}\:\Rightarrow\mid{z}\mid>\mathrm{1}\:{Meme}\:{Raisonnement}\:{Marche} \\ $$$$\left(\mathrm{2}\right)\:\frac{{z}^{{n}} }{\mathrm{1}+{z}^{\mathrm{2}{n}+\mathrm{1}} }=\underset{{k}\geqslant\mathrm{0}} {\sum}{z}^{{n}} \left(−{z}^{\mathrm{2}{n}+\mathrm{1}} \right)^{{k}} ;\forall\mid{z}\mid<\mathrm{1} \\ $$$${Soit}\:{S}=\Sigma{U}_{{n}} ,{S}\left({z}\right)=\underset{{n},{k}\geqslant\mathrm{0}} {\sum}{z}^{{n}} \left(−{z}^{\mathrm{2}{n}+\mathrm{1}} \right)^{{k}} =\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−{z}\right)^{{k}} \underset{{n}\geqslant\mathrm{0}} {\sum}{z}^{{n}\left(\mathrm{1}+\mathrm{2}{k}\right)} \\ $$$$\underset{{k}} {\sum}\underset{{n}} {\sum}=\underset{{n}} {\sum}\underset{{k}} {\sum}.....\left({On}\:{a}\:{Cv}\:{Absolut}\right)\: \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}{z}^{{n}\left(\mathrm{1}+\mathrm{2}{k}\right)} =\frac{\mathrm{1}}{\mathrm{1}−{z}^{\mathrm{1}+\mathrm{2}{k}} } \\ $$$${S}=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−{z}\right)^{{k}} }{\mathrm{1}−{z}^{\mathrm{1}+\mathrm{2}{k}} }={U}\left(−{z}\right) \\ $$$$\Rightarrow{s}\left({z}\right)={s}\left(−{z}\right),\forall\mid{z}\mid<\mathrm{1}\:{S}\:{pair}/{pour}\:\mid{z}\mid>\mathrm{1} \\ $$$${S}\left({z}\right)=\frac{{S}\left(\frac{\mathrm{1}}{{z}}\right)}{{z}},{s}\left(−{z}\right)=\frac{{s}\left(−\frac{\mathrm{1}}{{z}}\right)}{−{z}}=−\frac{{s}\left(\frac{\mathrm{1}}{{z}}\right)}{{z}}=−{s}\left({z}\right)\:\:{Impaire} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 23/Sep/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Commented by Ar Brandon last updated on 23/Sep/22
Thanks, comrade !
Commented by Peace last updated on 25/Sep/22
$${withe}\:{pleasur}\:{thank} \\ $$$${avec}\:{plaisir}\:{bonne}\:{journee} \\ $$
