
Question Number 176580 by mathlove last updated on 22/Sep/22
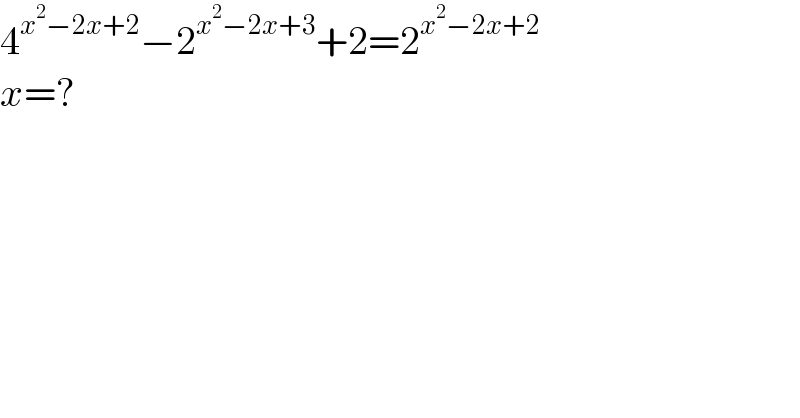
$$\mathrm{4}^{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}} −\mathrm{2}^{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3}} +\mathrm{2}=\mathrm{2}^{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}} \\ $$$${x}=? \\ $$
Answered by cortano1 last updated on 22/Sep/22
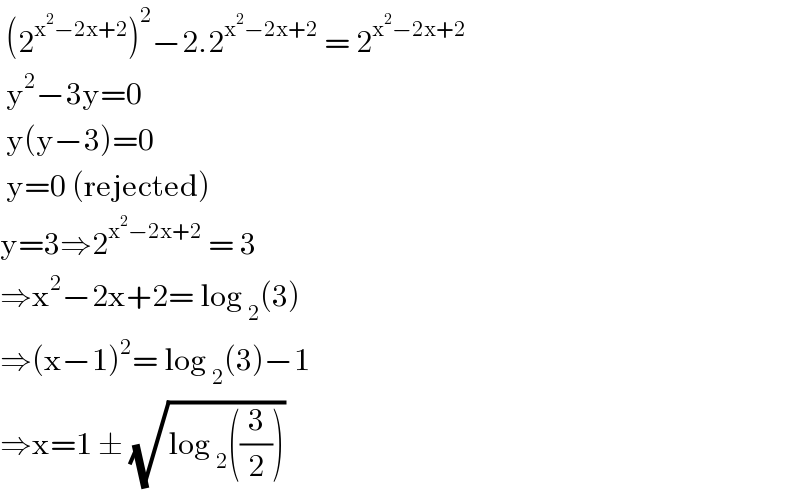
$$\:\left(\mathrm{2}^{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}.\mathrm{2}^{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}} \:=\:\mathrm{2}^{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}} \\ $$$$\:\mathrm{y}^{\mathrm{2}} −\mathrm{3y}=\mathrm{0} \\ $$$$\:\mathrm{y}\left(\mathrm{y}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\:\mathrm{y}=\mathrm{0}\:\left(\mathrm{rejected}\right) \\ $$$$\mathrm{y}=\mathrm{3}\Rightarrow\mathrm{2}^{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}} \:=\:\mathrm{3} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}=\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right) \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} =\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)−\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{1}\:\pm\:\sqrt{\mathrm{log}\:_{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$
