
Question Number 176570 by mathlove last updated on 21/Sep/22
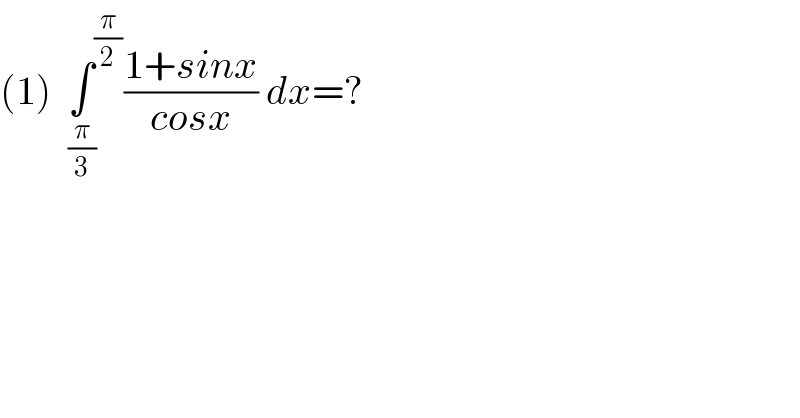
$$\left(\mathrm{1}\right)\:\:\underset{\frac{\pi}{\mathrm{3}}} {\int}^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+{sinx}}{{cosx}}\:{dx}=? \\ $$
Answered by Peace last updated on 21/Sep/22
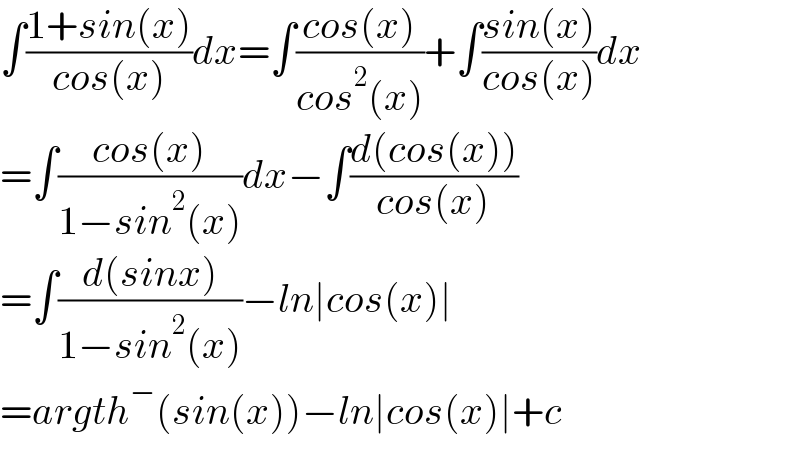
$$\int\frac{\mathrm{1}+{sin}\left({x}\right)}{{cos}\left({x}\right)}{dx}=\int\frac{{cos}\left({x}\right)}{{cos}^{\mathrm{2}} \left({x}\right)}+\int\frac{{sin}\left({x}\right)}{{cos}\left({x}\right)}{dx} \\ $$$$=\int\frac{{cos}\left({x}\right)}{\mathrm{1}−{sin}^{\mathrm{2}} \left({x}\right)}{dx}−\int\frac{{d}\left({cos}\left({x}\right)\right)}{{cos}\left({x}\right)} \\ $$$$=\int\frac{{d}\left({sinx}\right)}{\mathrm{1}−{sin}^{\mathrm{2}} \left({x}\right)}−{ln}\mid{cos}\left({x}\right)\mid \\ $$$$\underset{} {=}{argth}^{−} \left({sin}\left({x}\right)\right)−{ln}\mid{cos}\left({x}\right)\mid+{c} \\ $$
Answered by BaliramKumar last updated on 23/Sep/22
![∫[(1/2)sec^2 ((x/2))+tan((x/2))]dx = [tan((x/2))−2ln∣cos((x/2))∣]_(π/3) ^(π/2) = 1+ln(2)−(1/( (√3)))+2ln(((√3)/2)) = 1−ln(2)−(1/( (√3)))+ln(3) = 1−(1/( (√3))) + ln((3/2))](Q176635.png)
$$\int\left[\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right]{dx}\:=\:\left[{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{2}{ln}\mid{cos}\left(\frac{{x}}{\mathrm{2}}\right)\mid\underset{\frac{\pi}{\mathrm{3}}} {\overset{\frac{\pi}{\mathrm{2}}} {\right]}} \\ $$$$=\:\mathrm{1}+{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\mathrm{2}{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$=\:\mathrm{1}−{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+{ln}\left(\mathrm{3}\right) \\ $$$$=\:\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:+\:{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
