
Question Number 176531 by a.lgnaoui last updated on 20/Sep/22
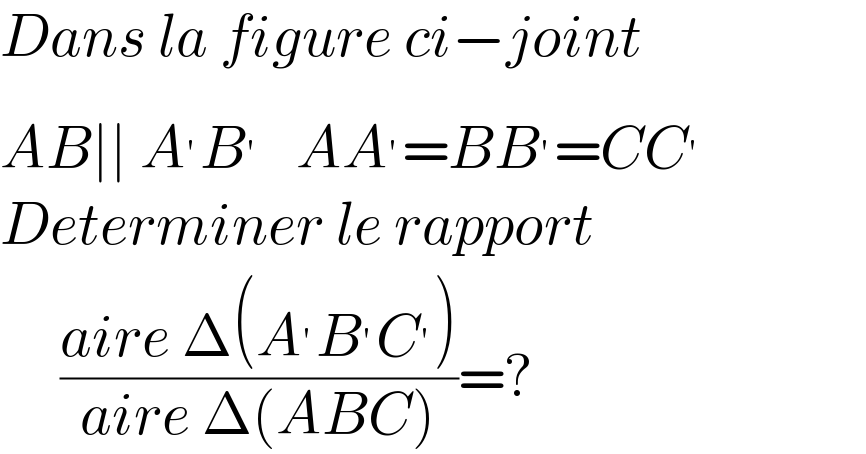
$${Dans}\:{la}\:{figure}\:{ci}−{joint} \\ $$$${AB}\mid\mid\:{A}^{'} {B}^{'} \:\:\:{AA}^{'} ={BB}^{'} ={CC}^{'} \\ $$$${Determiner}\:{le}\:{rapport} \\ $$$$\:\:\:\:\:\frac{{aire}\:\Delta\left({A}^{'} {B}^{'} {C}^{'} \right)}{{aire}\:\Delta\left({ABC}\right)}=? \\ $$
Commented by a.lgnaoui last updated on 20/Sep/22
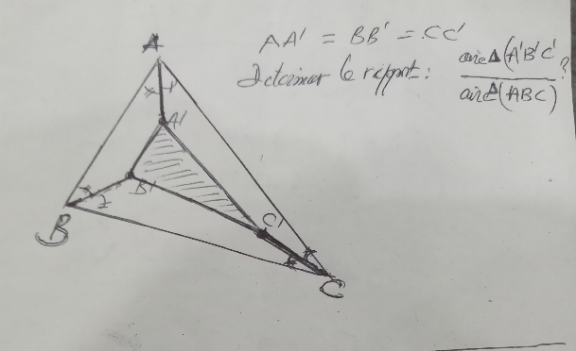
Commented by a.lgnaoui last updated on 20/Sep/22
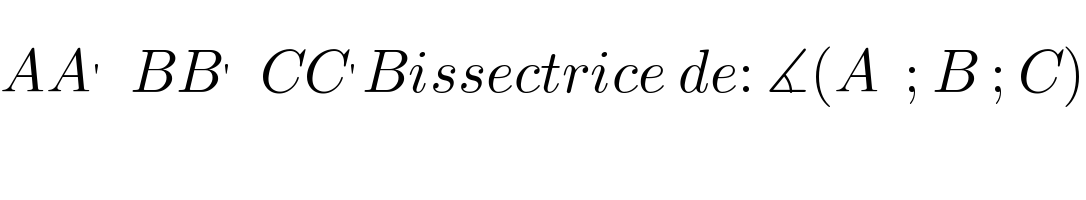
$${AA}^{'} \:\:{BB}^{'} \:\:{CC}^{'} {Bissectrice}\:{de}:\:\measuredangle\left({A}\:\:;\:{B}\:;\:{C}\right) \\ $$
Commented by mr W last updated on 20/Sep/22
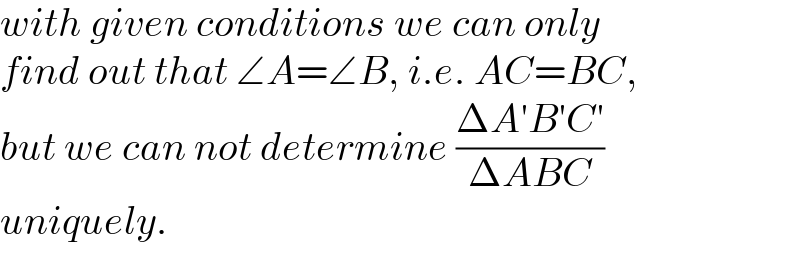
$${with}\:{given}\:{conditions}\:{we}\:{can}\:{only} \\ $$$${find}\:{out}\:{that}\:\angle{A}=\angle{B},\:{i}.{e}.\:{AC}={BC}, \\ $$$${but}\:{we}\:{can}\:{not}\:{determine}\:\frac{\Delta{A}'{B}'{C}'}{\Delta{ABC}} \\ $$$${uniquely}. \\ $$
Commented by a.lgnaoui last updated on 20/Sep/22

$${exactly} \\ $$
Answered by RahulRajpoot last updated on 20/Sep/22

$$ \\ $$
