
Question Number 176468 by blackmamba last updated on 20/Sep/22
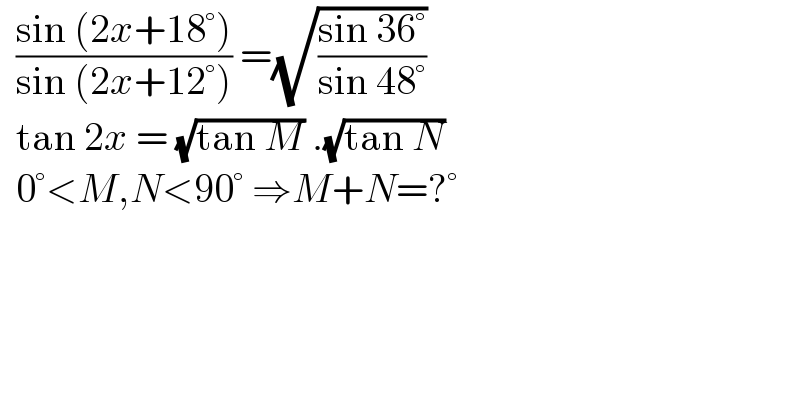
$$\:\:\frac{\mathrm{sin}\:\left(\mathrm{2}{x}+\mathrm{18}°\right)}{\mathrm{sin}\:\left(\mathrm{2}{x}+\mathrm{12}°\right)}\:=\sqrt{\frac{\mathrm{sin}\:\mathrm{36}°}{\mathrm{sin}\:\mathrm{48}°}}\: \\ $$ $$\:\:\mathrm{tan}\:\mathrm{2}{x}\:=\:\sqrt{\mathrm{tan}\:{M}}\:.\sqrt{\mathrm{tan}\:{N}} \\ $$ $$\:\:\mathrm{0}°<{M},{N}<\mathrm{90}°\:\Rightarrow{M}+{N}=?° \\ $$
Commented byPeace last updated on 20/Sep/22
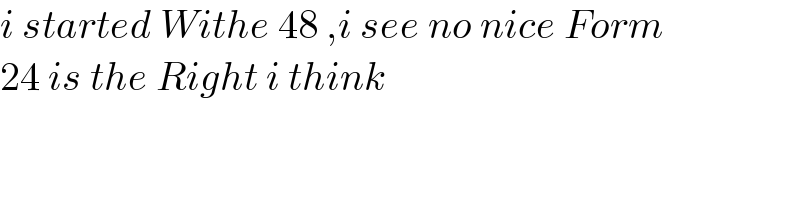
$${i}\:{started}\:{Withe}\:\mathrm{48}\:,{i}\:{see}\:{no}\:{nice}\:{Form} \\ $$ $$\mathrm{24}\:{is}\:{the}\:{Right}\:{i}\:{think} \\ $$
Answered by Peace last updated on 20/Sep/22

$$\frac{{sin}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{18}\right)+{cos}\left(\mathrm{2}{x}\right){sin}\left(\mathrm{18}\right)}{{sin}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{12}\right)+{cos}\left(\mathrm{2}{x}\right){sin}\left(\mathrm{12}\right)}=\sqrt{\frac{{sin}\left(\mathrm{2}.\mathrm{18}\right)}{{sin}\left(\mathrm{2}.\mathrm{12}\right)}} \\ $$ $$\Leftrightarrow\frac{{tg}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{18}\right)+{sin}\left(\mathrm{18}\right)}{{tg}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{12}\right)+\mathrm{sin}\left(\mathrm{12}\right)}=\sqrt{\frac{\mathrm{sin}\left(\mathrm{36}\right)}{\mathrm{sin}\left(\mathrm{24}\right)}=} \\ $$ $${t}={tg}\left(\mathrm{2}{x}\right) \\ $$ $$\Leftrightarrow\frac{{tg}\left(\mathrm{2}{x}\right)+{tg}\left(\mathrm{18}\right)}{{tg}\left(\mathrm{2}{x}\right)+{tg}\left(\mathrm{12}\right)}=\frac{{cos}\left(\mathrm{12}\right)}{{cos}\left(\mathrm{18}\right)}.\sqrt{\frac{{sin}\left(\mathrm{36}\right)}{{sin}\left(\mathrm{48}\right)}}=\sqrt{\frac{{sin}\left(\mathrm{36}\right){cos}^{\mathrm{2}} \left(\mathrm{12}\right)}{{cos}^{\mathrm{2}} \left(\mathrm{18}\right){sin}\left(\mathrm{24}\right)}} \\ $$ $$=\sqrt{\frac{\mathrm{2}{sin}\left(\mathrm{18}\right){cos}\left(\mathrm{18}\right){cos}^{\mathrm{2}} \left(\mathrm{12}\right)}{{cos}^{\mathrm{2}} \left(\mathrm{18}\right).\mathrm{2}{sin}\left(\mathrm{24}\right){cos}\left(\mathrm{24}\right)}} \\ $$ $$=\sqrt{\frac{{tg}\left(\mathrm{18}\right){cos}^{\mathrm{2}} \left(\mathrm{12}\right)}{\mathrm{2}{sin}\left(\mathrm{12}\right){cos}\left(\mathrm{12}\right)}}=\sqrt{\frac{{tg}\left(\mathrm{18}\right)}{{tg}\left(\mathrm{12}\right)}} \\ $$ $$\frac{{t}+{tg}\left(\mathrm{18}\right)}{{t}+{tg}\left(\mathrm{12}\right)}={c}\Rightarrow{t}\left(\mathrm{1}−{c}\right)={ctg}\left(\mathrm{12}\right)−{tg}\left(\mathrm{18}\right)\Rightarrow{tg}\left(\mathrm{2}{x}\right)=\frac{{ctg}\left(\mathrm{12}\right)−{tg}\left(\mathrm{18}\right)}{{c}−\mathrm{1}} \\ $$ $$\frac{\sqrt{{tg}\left(\mathrm{18}\right){tg}\left(\mathrm{12}\right)}−{tg}\left(\mathrm{18}\right)}{\mathrm{1}−\sqrt{\frac{{tg}\left(\mathrm{18}\right)}{{tg}\left(\mathrm{12}\right)}}}=\frac{\sqrt{{tg}\left(\mathrm{18}\right)}\left(\sqrt{{tg}\left(\mathrm{12}\right.}−\sqrt{{tg}\left(\mathrm{18}\right)}\right)}{\:\sqrt{{tg}\left(\mathrm{12}\right)}−\sqrt{{tg}\left(\mathrm{18}\right)}}.\sqrt{{tg}\left(\mathrm{12}\right)} \\ $$ $$=\sqrt{{tg}\left(\mathrm{18}\right){tg}\left(\mathrm{12}\right)} \\ $$ $${M}+{N}=\mathrm{30} \\ $$ $$ \\ $$ $$ \\ $$
Commented byblackmamba last updated on 26/Sep/22

$${wrong} \\ $$
