
Question Number 176458 by mathlove last updated on 19/Sep/22

$${x}^{\mathrm{2}} +{x}=\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{5}} +\mathrm{8}}{{x}+\mathrm{1}}=? \\ $$
Answered by Rasheed.Sindhi last updated on 19/Sep/22
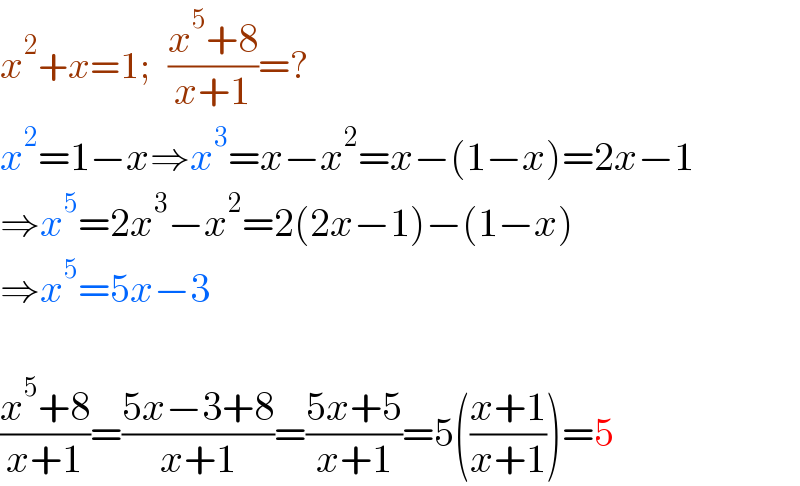
$${x}^{\mathrm{2}} +{x}=\mathrm{1};\:\:\:\frac{{x}^{\mathrm{5}} +\mathrm{8}}{{x}+\mathrm{1}}=? \\ $$$${x}^{\mathrm{2}} =\mathrm{1}−{x}\Rightarrow{x}^{\mathrm{3}} ={x}−{x}^{\mathrm{2}} ={x}−\left(\mathrm{1}−{x}\right)=\mathrm{2}{x}−\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{5}} =\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{2}{x}−\mathrm{1}\right)−\left(\mathrm{1}−{x}\right) \\ $$$$\Rightarrow{x}^{\mathrm{5}} =\mathrm{5}{x}−\mathrm{3} \\ $$$$ \\ $$$$\frac{{x}^{\mathrm{5}} +\mathrm{8}}{{x}+\mathrm{1}}=\frac{\mathrm{5}{x}−\mathrm{3}+\mathrm{8}}{{x}+\mathrm{1}}=\frac{\mathrm{5}{x}+\mathrm{5}}{{x}+\mathrm{1}}=\mathrm{5}\left(\frac{{x}+\mathrm{1}}{{x}+\mathrm{1}}\right)=\mathrm{5} \\ $$
Commented by mathlove last updated on 20/Sep/22

$${thanks} \\ $$
Answered by Rasheed.Sindhi last updated on 20/Sep/22

$$\:\:\:\:\:\:\underset{\left(\mathcal{R}{eplacing}\:\mathrm{1}'\boldsymbol{\mathrm{s}}\:\right)} {\:\boldsymbol{\mathrm{AnOther}}\:\boldsymbol{\mathrm{way}}...} \\ $$$$\begin{array}{|c|}{{x}^{\mathrm{2}} +{x}=\mathrm{1};\:\:\:\frac{{x}^{\mathrm{5}} +\mathrm{8}}{{x}+\mathrm{1}}=?}\\\hline\end{array} \\ $$$$\frac{{x}^{\mathrm{5}} +\mathrm{8}}{{x}+\mathrm{1}}=\frac{{x}^{\mathrm{5}} +\mathrm{8}\left({x}^{\mathrm{2}} +{x}\right)}{{x}+{x}^{\mathrm{2}} +{x}}=\frac{{x}^{\mathrm{5}} +\mathrm{8}{x}^{\mathrm{2}} +\mathrm{8}{x}}{{x}^{\mathrm{2}} +\mathrm{2}{x}} \\ $$$$=\frac{{x}^{\mathrm{4}} +\mathrm{8}{x}+\mathrm{8}}{{x}+\mathrm{2}}=\frac{{x}^{\mathrm{4}} +\mathrm{8}{x}+\mathrm{8}\left({x}^{\mathrm{2}} +{x}\right)}{{x}+\mathrm{2}\left({x}^{\mathrm{2}} +{x}\right)}\:=\frac{{x}^{\mathrm{4}} +\mathrm{8}{x}^{\mathrm{2}} +\mathrm{16}{x}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}} \\ $$$$=\frac{{x}^{\mathrm{3}} +\mathrm{8}{x}+\mathrm{16}}{\mathrm{2}{x}+\mathrm{3}}=\frac{{x}^{\mathrm{3}} +\mathrm{8}{x}+\mathrm{16}\left({x}^{\mathrm{2}} +{x}\right)}{\mathrm{2}{x}+\mathrm{3}\left({x}^{\mathrm{2}} +{x}\right)}=\frac{{x}^{\mathrm{3}} +\mathrm{16}{x}^{\mathrm{2}} +\mathrm{24}{x}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{5}{x}} \\ $$$$=\frac{{x}^{\mathrm{2}} +\mathrm{16}{x}+\mathrm{24}}{\mathrm{3}{x}+\mathrm{5}}=\frac{{x}^{\mathrm{2}} +\mathrm{16}{x}+\mathrm{24}\left({x}^{\mathrm{2}} +{x}\right)}{\mathrm{3}{x}+\mathrm{5}\left({x}^{\mathrm{2}} +{x}\right)} \\ $$$$=\frac{\mathrm{25}{x}^{\mathrm{2}} +\mathrm{40}{x}}{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{8}{x}}=\frac{\mathrm{25}{x}+\mathrm{40}}{\mathrm{5}{x}+\mathrm{8}}=\frac{\mathrm{5}\cancel{\left(\mathrm{5}{x}+\mathrm{8}\right)}}{\cancel{\left(\mathrm{5}{x}+\mathrm{8}\right)}} \\ $$$$=\mathrm{5} \\ $$
Answered by Rasheed.Sindhi last updated on 20/Sep/22
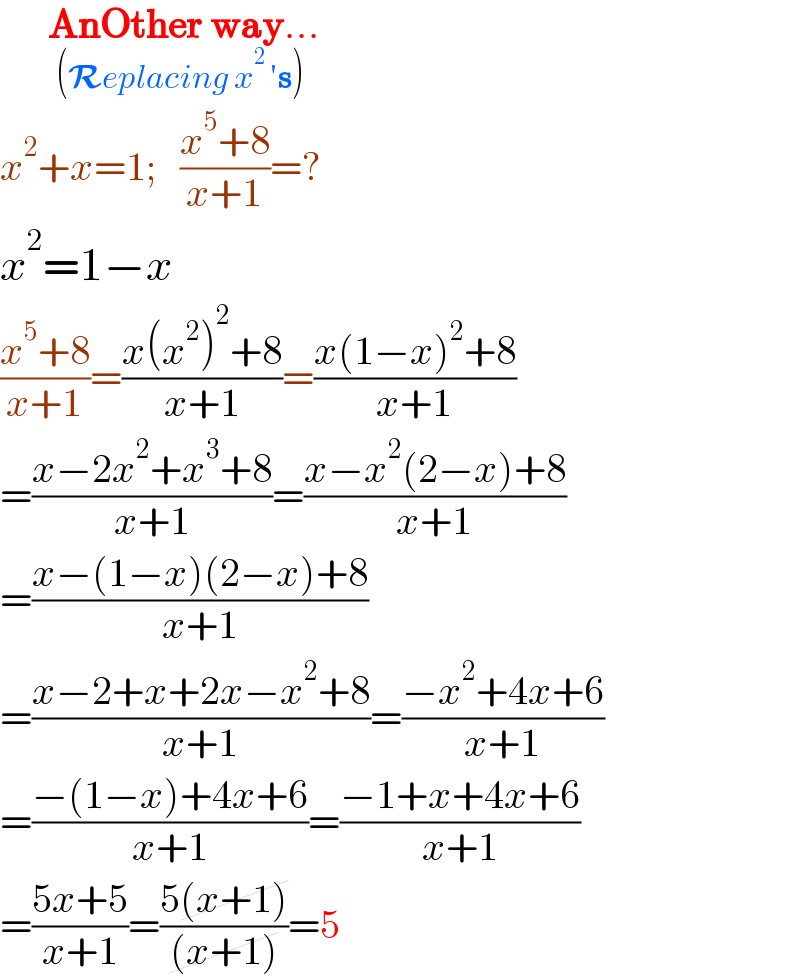
$$\:\:\:\:\:\underset{\left(\boldsymbol{\mathcal{R}}{eplacing}\:{x}^{\mathrm{2}\:} '\boldsymbol{\mathrm{s}}\right)} {\:\boldsymbol{\mathrm{AnOther}}\:\boldsymbol{\mathrm{way}}...} \\ $$$${x}^{\mathrm{2}} +{x}=\mathrm{1};\:\:\:\frac{{x}^{\mathrm{5}} +\mathrm{8}}{{x}+\mathrm{1}}=? \\ $$$${x}^{\mathrm{2}} =\mathrm{1}−{x} \\ $$$$\frac{{x}^{\mathrm{5}} +\mathrm{8}}{{x}+\mathrm{1}}=\frac{{x}\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{8}}{{x}+\mathrm{1}}=\frac{{x}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +\mathrm{8}}{{x}+\mathrm{1}} \\ $$$$=\frac{{x}−\mathrm{2}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +\mathrm{8}}{{x}+\mathrm{1}}=\frac{{x}−{x}^{\mathrm{2}} \left(\mathrm{2}−{x}\right)+\mathrm{8}}{{x}+\mathrm{1}} \\ $$$$=\frac{{x}−\left(\mathrm{1}−{x}\right)\left(\mathrm{2}−{x}\right)+\mathrm{8}}{{x}+\mathrm{1}} \\ $$$$=\frac{{x}−\mathrm{2}+{x}+\mathrm{2}{x}−{x}^{\mathrm{2}} +\mathrm{8}}{{x}+\mathrm{1}}=\frac{−{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{6}}{{x}+\mathrm{1}} \\ $$$$=\frac{−\left(\mathrm{1}−{x}\right)+\mathrm{4}{x}+\mathrm{6}}{{x}+\mathrm{1}}=\frac{−\mathrm{1}+{x}+\mathrm{4}{x}+\mathrm{6}}{{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{5}{x}+\mathrm{5}}{{x}+\mathrm{1}}=\frac{\mathrm{5}\cancel{\left({x}+\mathrm{1}\right)}}{\cancel{\left({x}+\mathrm{1}\right)}}=\mathrm{5} \\ $$
Answered by Rasheed.Sindhi last updated on 20/Sep/22
![A_(pproach) ^(nOther) ... x^2 +x=1; ((x^5 +8)/(x+1))=? determinant (((x(x+1)=1))) ((x^5 +8)/(x+1)) =((x(x^5 +8))/(x(x+1))) [x(x+1)=1] =x^6 +x^5 −x^5 +8x =x^5 (x+1)−x^5 +8x =x^4 ∙x(x+1)−x^5 +8x =x^4 +x^4 −x^5 −x^4 +8x =2x^4 −x^3 .x(x+1)+8x =2x^4 +2x^3 −3x^3 +8x =2x^2 .x(x+1)−3x^3 +8x =5x^2 −3x^3 −3x^2 +8x =5x^2 −3x.x(x+1)+8x =5x^2 −3x+8x =5x^2 +5x =5x(x+1) =5](Q176497.png)
$$\mathbb{A}_{\boldsymbol{\mathrm{pproach}}} ^{\boldsymbol{\mathrm{nOther}}} \:... \\ $$$${x}^{\mathrm{2}} +{x}=\mathrm{1};\:\:\:\:\frac{{x}^{\mathrm{5}} +\mathrm{8}}{{x}+\mathrm{1}}=? \\ $$$$\begin{array}{|c|}{{x}\left({x}+\mathrm{1}\right)=\mathrm{1}}\\\hline\end{array} \\ $$$$\frac{{x}^{\mathrm{5}} +\mathrm{8}}{{x}+\mathrm{1}} \\ $$$$=\frac{{x}\left({x}^{\mathrm{5}} +\mathrm{8}\right)}{{x}\left({x}+\mathrm{1}\right)}\:\:\:\:\:\:\:\:\left[{x}\left({x}+\mathrm{1}\right)=\mathrm{1}\right] \\ $$$$={x}^{\mathrm{6}} +{x}^{\mathrm{5}} −{x}^{\mathrm{5}} +\mathrm{8}{x} \\ $$$$={x}^{\mathrm{5}} \left({x}+\mathrm{1}\right)−{x}^{\mathrm{5}} +\mathrm{8}{x} \\ $$$$={x}^{\mathrm{4}} \centerdot{x}\left({x}+\mathrm{1}\right)−{x}^{\mathrm{5}} +\mathrm{8}{x} \\ $$$$={x}^{\mathrm{4}} +{x}^{\mathrm{4}} −{x}^{\mathrm{5}} −{x}^{\mathrm{4}} +\mathrm{8}{x} \\ $$$$=\mathrm{2}{x}^{\mathrm{4}} −{x}^{\mathrm{3}} .{x}\left({x}+\mathrm{1}\right)+\mathrm{8}{x} \\ $$$$=\mathrm{2}{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{8}{x} \\ $$$$=\mathrm{2}{x}^{\mathrm{2}} .{x}\left({x}+\mathrm{1}\right)−\mathrm{3}{x}^{\mathrm{3}} +\mathrm{8}{x} \\ $$$$=\mathrm{5}{x}^{\mathrm{2}} −\mathrm{3}{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{8}{x} \\ $$$$=\mathrm{5}{x}^{\mathrm{2}} −\mathrm{3}{x}.{x}\left({x}+\mathrm{1}\right)+\mathrm{8}{x} \\ $$$$=\mathrm{5}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{8}{x} \\ $$$$=\mathrm{5}{x}^{\mathrm{2}} +\mathrm{5}{x} \\ $$$$=\mathrm{5}{x}\left({x}+\mathrm{1}\right) \\ $$$$=\mathrm{5} \\ $$
Commented by Tawa11 last updated on 20/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 20/Sep/22

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{miss}} \\ $$
Commented by mathlove last updated on 02/Oct/22

$${thanks}\:{a}\:{lot} \\ $$
Answered by Peace last updated on 20/Sep/22
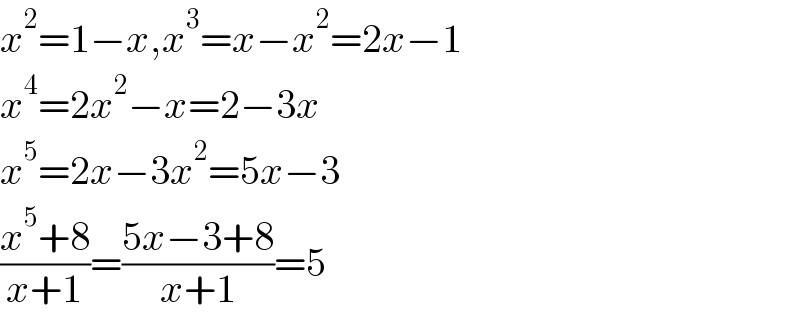
$${x}^{\mathrm{2}} =\mathrm{1}−{x},{x}^{\mathrm{3}} ={x}−{x}^{\mathrm{2}} =\mathrm{2}{x}−\mathrm{1} \\ $$$${x}^{\mathrm{4}} =\mathrm{2}{x}^{\mathrm{2}} −{x}=\mathrm{2}−\mathrm{3}{x} \\ $$$${x}^{\mathrm{5}} =\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} =\mathrm{5}{x}−\mathrm{3} \\ $$$$\frac{{x}^{\mathrm{5}} +\mathrm{8}}{{x}+\mathrm{1}}=\frac{\mathrm{5}{x}−\mathrm{3}+\mathrm{8}}{{x}+\mathrm{1}}=\mathrm{5} \\ $$
