
Question Number 176453 by mnjuly1970 last updated on 19/Sep/22
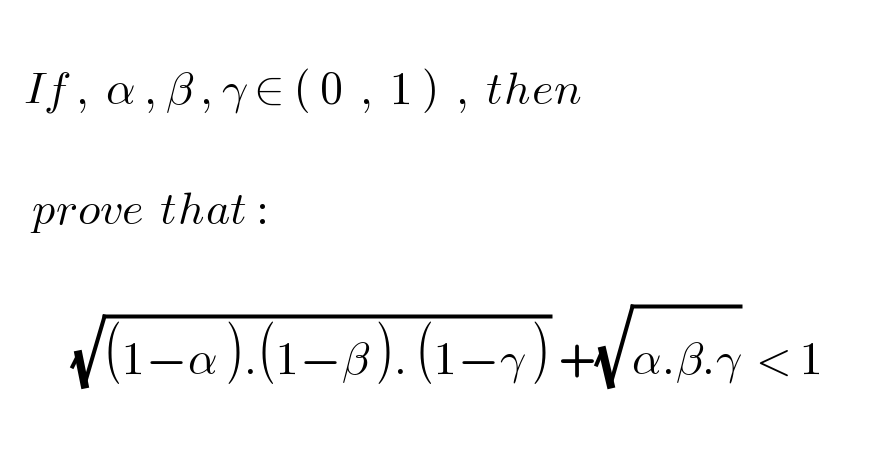
$$ \\ $$ $$\:\:\:{If}\:,\:\:\alpha\:,\:\beta\:,\:\gamma\:\in\:\left(\:\mathrm{0}\:\:,\:\:\mathrm{1}\:\right)\:\:,\:\:{then}\: \\ $$ $$\:\:\:\: \\ $$ $$\:\:\:\:{prove}\:\:{that}\::\:\: \\ $$ $$ \\ $$ $$\:\:\:\:\:\:\:\:\:\sqrt{\left(\mathrm{1}\overset{} {−}\alpha\:\right).\left(\mathrm{1}\overset{} {−}\beta\:\right).\:\left(\mathrm{1}\overset{} {−}\gamma\:\right)}\:+\sqrt{\overset{} {\alpha}.\overset{} {\beta}.\overset{} {\gamma}}\:\:<\:\mathrm{1} \\ $$ $$\:\:\:\:\:\: \\ $$
Answered by ajfour last updated on 19/Sep/22
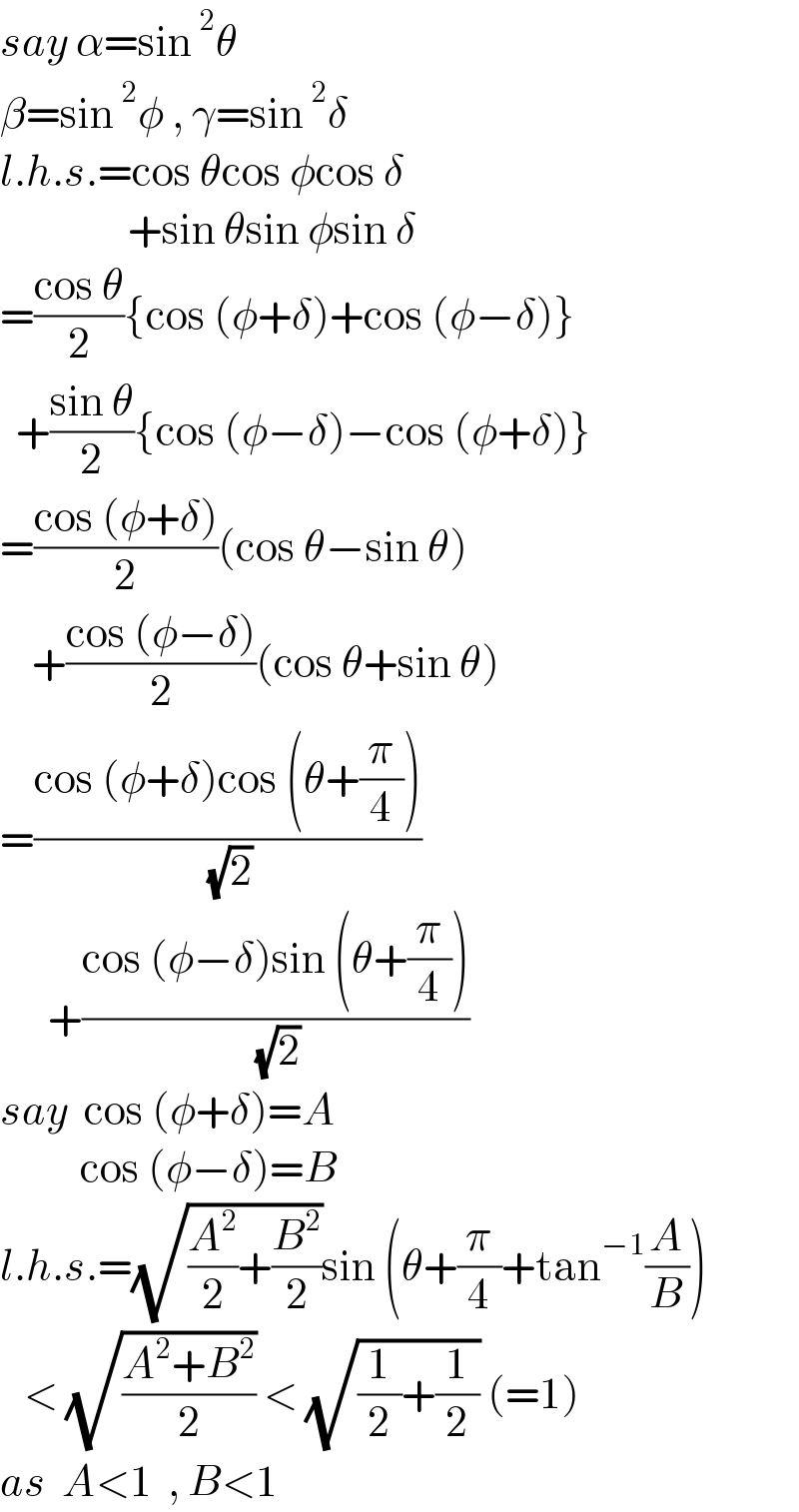
$${say}\:\alpha=\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$ $$\beta=\mathrm{sin}\:^{\mathrm{2}} \phi\:,\:\gamma=\mathrm{sin}\:^{\mathrm{2}} \delta \\ $$ $${l}.{h}.{s}.=\mathrm{cos}\:\theta\mathrm{cos}\:\phi\mathrm{cos}\:\delta \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{sin}\:\theta\mathrm{sin}\:\phi\mathrm{sin}\:\delta \\ $$ $$=\frac{\mathrm{cos}\:\theta}{\mathrm{2}}\left\{\mathrm{cos}\:\left(\phi+\delta\right)+\mathrm{cos}\:\left(\phi−\delta\right)\right\} \\ $$ $$\:\:+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\left\{\mathrm{cos}\:\left(\phi−\delta\right)−\mathrm{cos}\:\left(\phi+\delta\right)\right\} \\ $$ $$=\frac{\mathrm{cos}\:\left(\phi+\delta\right)}{\mathrm{2}}\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right) \\ $$ $$\:\:\:\:+\frac{\mathrm{cos}\:\left(\phi−\delta\right)}{\mathrm{2}}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right) \\ $$ $$=\frac{\mathrm{cos}\:\left(\phi+\delta\right)\mathrm{cos}\:\left(\theta+\frac{\pi}{\mathrm{4}}\right)}{\:\sqrt{\mathrm{2}}} \\ $$ $$\:\:\:\:\:\:+\frac{\mathrm{cos}\:\left(\phi−\delta\right)\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{4}}\right)}{\:\sqrt{\mathrm{2}}} \\ $$ $${say}\:\:\mathrm{cos}\:\left(\phi+\delta\right)={A} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\left(\phi−\delta\right)={B} \\ $$ $${l}.{h}.{s}.=\sqrt{\frac{{A}^{\mathrm{2}} }{\mathrm{2}}+\frac{{B}^{\mathrm{2}} }{\mathrm{2}}}\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{4}}+\mathrm{tan}^{−\mathrm{1}} \frac{{A}}{{B}}\right) \\ $$ $$\:\:\:<\:\sqrt{\frac{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }{\mathrm{2}}}\:<\:\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}\:\left(=\mathrm{1}\right) \\ $$ $${as}\:\:{A}<\mathrm{1}\:\:,\:{B}<\mathrm{1} \\ $$
Commented byajfour last updated on 19/Sep/22
https://youtu.be/86aXbrp2ZG0
Commented byajfour last updated on 19/Sep/22

$${A}\:{small}\:{experimental}\:{educational} \\ $$ $$\:{video}\:{of}\:{mine}\:{on}\:{youtube}.. \\ $$
Commented bymnjuly1970 last updated on 19/Sep/22
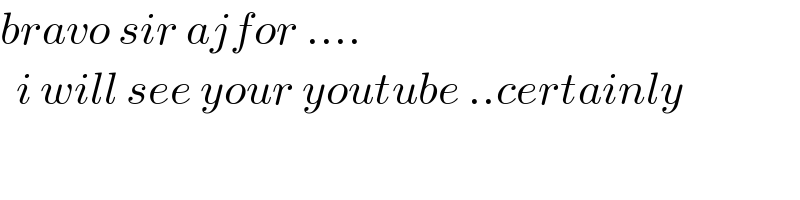
$${bravo}\:{sir}\:{ajfor}\:.... \\ $$ $$\:\:{i}\:{will}\:{see}\:{your}\:{youtube}\:..{certainly} \\ $$
Commented byTawa11 last updated on 20/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 19/Sep/22
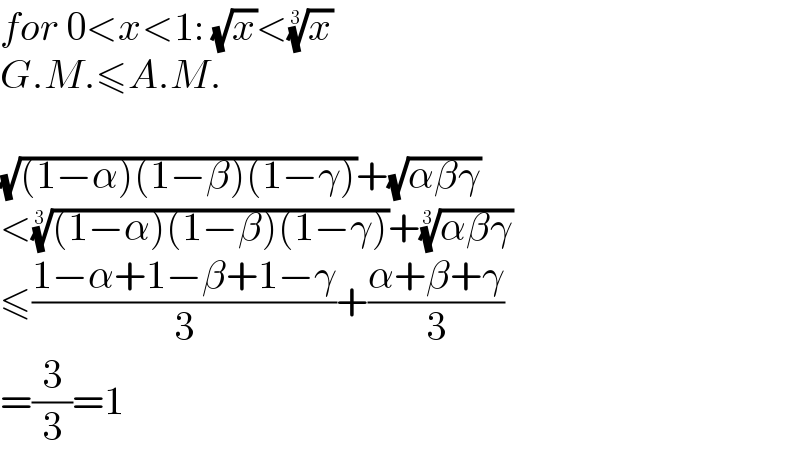
$${for}\:\mathrm{0}<{x}<\mathrm{1}:\:\sqrt{{x}}<\sqrt[{\mathrm{3}}]{{x}} \\ $$ $${G}.{M}.\leqslant{A}.{M}. \\ $$ $$ \\ $$ $$\sqrt{\left(\mathrm{1}−\alpha\right)\left(\mathrm{1}−\beta\right)\left(\mathrm{1}−\gamma\right)}+\sqrt{\alpha\beta\gamma} \\ $$ $$<\sqrt[{\mathrm{3}}]{\left(\mathrm{1}−\alpha\right)\left(\mathrm{1}−\beta\right)\left(\mathrm{1}−\gamma\right)}+\sqrt[{\mathrm{3}}]{\alpha\beta\gamma} \\ $$ $$\leqslant\frac{\mathrm{1}−\alpha+\mathrm{1}−\beta+\mathrm{1}−\gamma}{\mathrm{3}}+\frac{\alpha+\beta+\gamma}{\mathrm{3}} \\ $$ $$=\frac{\mathrm{3}}{\mathrm{3}}=\mathrm{1} \\ $$
Commented bymnjuly1970 last updated on 19/Sep/22
$${bravo}\:{sir}\:{W}...{thanks}\:{alot} \\ $$
Commented byTawa11 last updated on 20/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
