
Question Number 176423 by Shrinava last updated on 18/Sep/22
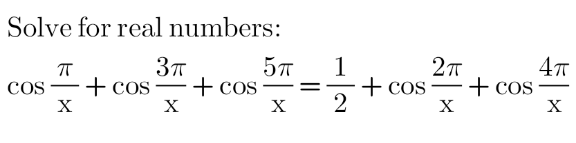
Answered by a.lgnaoui last updated on 21/Sep/22
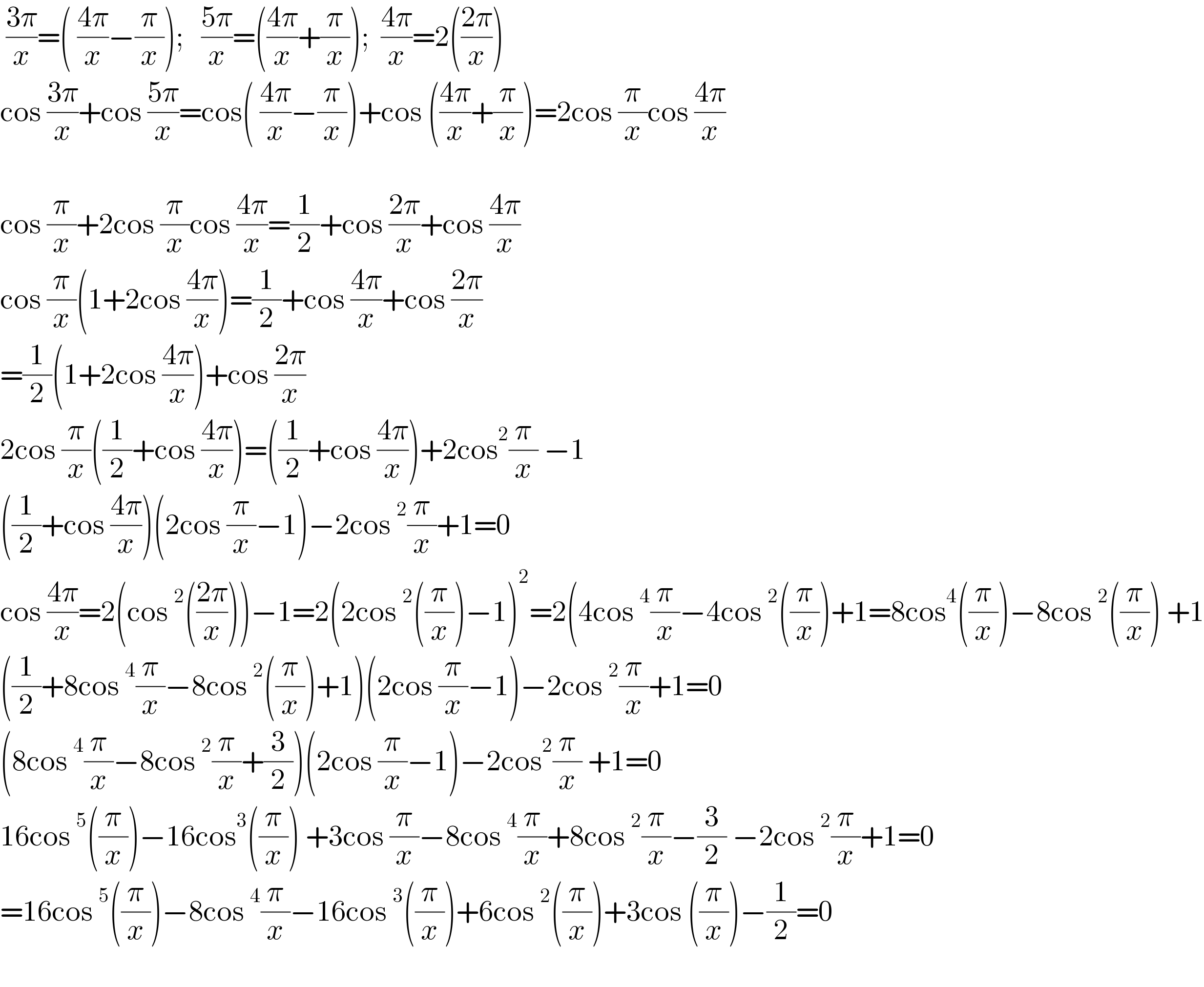
$$\:\frac{\mathrm{3}\pi}{{x}}=\left(\:\frac{\mathrm{4}\pi}{{x}}−\frac{\pi}{{x}}\right);\:\:\:\frac{\mathrm{5}\pi}{{x}}=\left(\frac{\mathrm{4}\pi}{{x}}+\frac{\pi}{{x}}\right);\:\:\frac{\mathrm{4}\pi}{{x}}=\mathrm{2}\left(\frac{\mathrm{2}\pi}{{x}}\right)\:\:\: \\ $$$$\mathrm{cos}\:\frac{\mathrm{3}\pi}{{x}}+\mathrm{cos}\:\frac{\mathrm{5}\pi}{{x}}=\mathrm{cos}\left(\:\frac{\mathrm{4}\pi}{{x}}−\frac{\pi}{{x}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{{x}}+\frac{\pi}{{x}}\right)=\mathrm{2cos}\:\frac{\pi}{{x}}\mathrm{cos}\:\frac{\mathrm{4}\pi}{{x}} \\ $$$$ \\ $$$$\mathrm{cos}\:\frac{\pi}{{x}}+\mathrm{2cos}\:\frac{\pi}{{x}}\mathrm{cos}\:\frac{\mathrm{4}\pi}{{x}}=\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{2}\pi}{{x}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{{x}} \\ $$$$\mathrm{cos}\:\frac{\pi}{{x}}\left(\mathrm{1}+\mathrm{2cos}\:\frac{\mathrm{4}\pi}{{x}}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{{x}}+\mathrm{cos}\:\frac{\mathrm{2}\pi}{{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2cos}\:\frac{\mathrm{4}\pi}{{x}}\right)+\mathrm{cos}\:\frac{\mathrm{2}\pi}{{x}} \\ $$$$\mathrm{2cos}\:\frac{\pi}{{x}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{{x}}\right)=\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{{x}}\right)+\mathrm{2cos}^{\mathrm{2}} \frac{\pi}{{x}}\:−\mathrm{1} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{{x}}\right)\left(\mathrm{2cos}\:\frac{\pi}{{x}}−\mathrm{1}\right)−\mathrm{2cos}\:^{\mathrm{2}} \frac{\pi}{{x}}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{cos}\:\frac{\mathrm{4}\pi}{{x}}=\mathrm{2}\left(\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\mathrm{2}\pi}{{x}}\right)\right)−\mathrm{1}=\mathrm{2}\left(\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\pi}{{x}}\right)−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{4cos}\:^{\mathrm{4}} \frac{\pi}{{x}}−\mathrm{4cos}\:^{\mathrm{2}} \left(\frac{\pi}{{x}}\right)+\mathrm{1}=\mathrm{8cos}^{\mathrm{4}} \left(\frac{\pi}{{x}}\right)−\mathrm{8cos}\:^{\mathrm{2}} \left(\frac{\pi}{{x}}\right)\:+\mathrm{1}\right. \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{8cos}\:^{\mathrm{4}} \frac{\pi}{{x}}−\mathrm{8cos}\:^{\mathrm{2}} \left(\frac{\pi}{{x}}\right)+\mathrm{1}\right)\left(\mathrm{2cos}\:\frac{\pi}{{x}}−\mathrm{1}\right)−\mathrm{2cos}\:^{\mathrm{2}} \frac{\pi}{{x}}+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{8cos}\:^{\mathrm{4}} \frac{\pi}{{x}}−\mathrm{8cos}\:^{\mathrm{2}} \frac{\pi}{{x}}+\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\mathrm{2cos}\:\frac{\pi}{{x}}−\mathrm{1}\right)−\mathrm{2cos}^{\mathrm{2}} \frac{\pi}{{x}}\:+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{16cos}\:^{\mathrm{5}} \left(\frac{\pi}{{x}}\right)−\mathrm{16cos}^{\mathrm{3}} \left(\frac{\pi}{{x}}\right)\:+\mathrm{3cos}\:\frac{\pi}{{x}}−\mathrm{8cos}\:^{\mathrm{4}} \frac{\pi}{{x}}+\mathrm{8cos}\:^{\mathrm{2}} \frac{\pi}{{x}}−\frac{\mathrm{3}}{\mathrm{2}}\:−\mathrm{2cos}\:^{\mathrm{2}} \frac{\pi}{{x}}+\mathrm{1}=\mathrm{0} \\ $$$$=\mathrm{16cos}\:^{\mathrm{5}} \left(\frac{\pi}{{x}}\right)−\mathrm{8cos}\:^{\mathrm{4}} \frac{\pi}{{x}}−\mathrm{16cos}\:^{\mathrm{3}} \left(\frac{\pi}{{x}}\right)+\mathrm{6cos}\:^{\mathrm{2}} \left(\frac{\pi}{{x}}\right)+\mathrm{3cos}\:\left(\frac{\pi}{{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 21/Sep/22
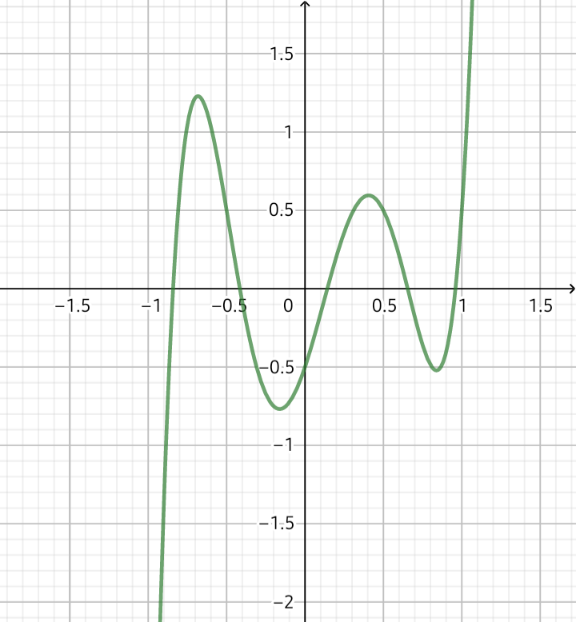
Commented by a.lgnaoui last updated on 21/Sep/22
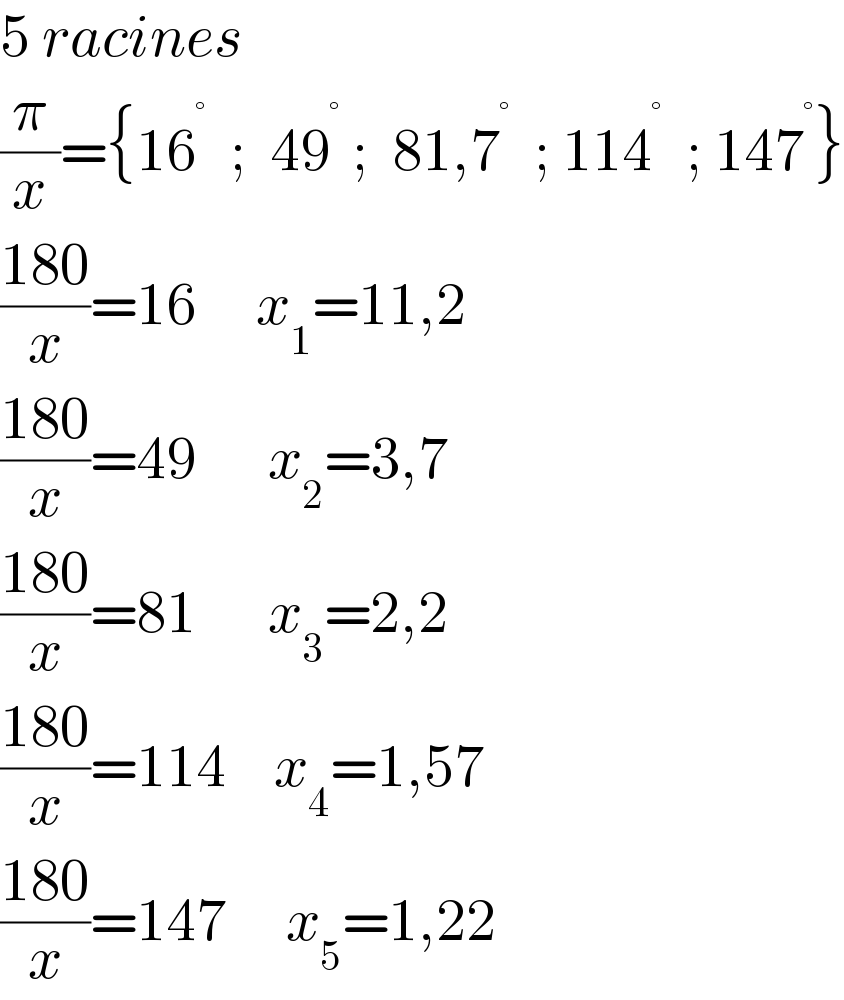
$$\mathrm{5}\:{racines} \\ $$$$\frac{\pi}{{x}}=\left\{\mathrm{16}^{°} \:\:;\:\:\mathrm{49}^{°} \:;\:\:\mathrm{81},\mathrm{7}^{°} \:\:;\:\mathrm{114}^{°} \:\:;\:\mathrm{147}^{°} \right\} \\ $$$$\frac{\mathrm{180}}{{x}}=\mathrm{16}\:\:\:\:\:{x}_{\mathrm{1}} =\mathrm{11},\mathrm{2} \\ $$$$\frac{\mathrm{180}}{{x}}=\mathrm{49}\:\:\:\:\:\:{x}_{\mathrm{2}} =\mathrm{3},\mathrm{7} \\ $$$$\frac{\mathrm{180}}{{x}}=\mathrm{81}\:\:\:\:\:\:{x}_{\mathrm{3}} =\mathrm{2},\mathrm{2} \\ $$$$\frac{\mathrm{180}}{{x}}=\mathrm{114}\:\:\:\:{x}_{\mathrm{4}} =\mathrm{1},\mathrm{57} \\ $$$$\frac{\mathrm{180}}{{x}}=\mathrm{147}\:\:\:\:\:{x}_{\mathrm{5}} =\mathrm{1},\mathrm{22} \\ $$
Commented by Shrinava last updated on 23/Sep/22
$$\mathrm{Cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{professor},\:\mathrm{thank}\:\mathrm{you}, \\ $$$$\mathrm{answer}\:\mathrm{5}\:\mathrm{root}.? \\ $$
Commented by a.lgnaoui last updated on 23/Sep/22
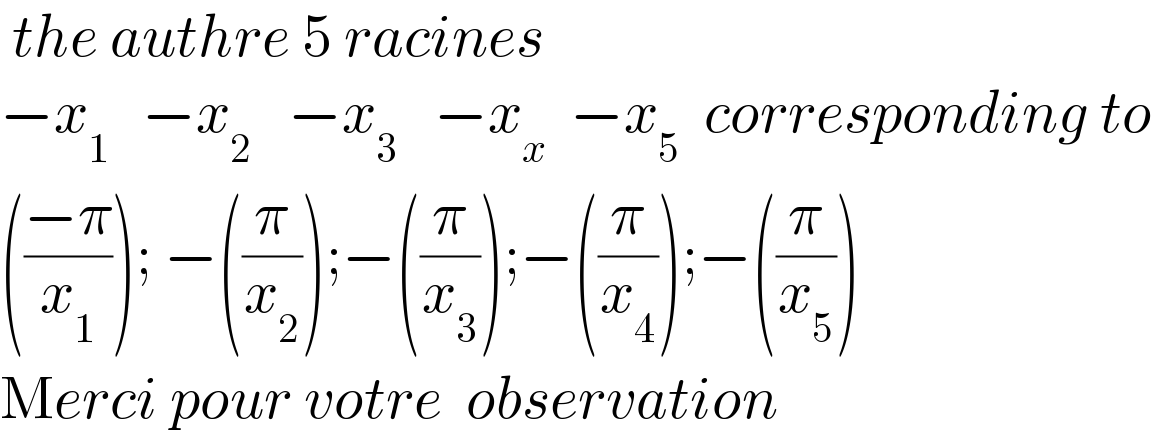
$$\:{the}\:{authre}\:\mathrm{5}\:{racines} \\ $$$$−{x}_{\mathrm{1}\:} \:\:−{x}_{\mathrm{2}} \:\:\:−{x}_{\mathrm{3}} \:\:\:−{x}_{{x}} \:\:−{x}_{\mathrm{5}} \:\:{corresponding}\:{to} \\ $$$$\left(\frac{−\pi}{{x}_{\mathrm{1}} }\right);\:−\left(\frac{\pi}{{x}_{\mathrm{2}} }\right);−\left(\frac{\pi}{{x}_{\mathrm{3}} }\right);−\left(\frac{\pi}{{x}_{\mathrm{4}} }\right);−\left(\frac{\pi}{{x}_{\mathrm{5}} }\right) \\ $$$$\mathrm{M}{erci}\:{pour}\:{votre}\:\:{observation} \\ $$
Commented by Shrinava last updated on 25/Sep/22
$$\mathrm{Thankyou}\:\mathrm{dear}\:\mathrm{professor},\:\mathrm{answer}?\:\mathrm{please} \\ $$
