
Question Number 176366 by doline last updated on 17/Sep/22

$${donner}\:{la}\:{forme}\:{trigonometrique}\:{de}\left(\mathrm{1}−{i}\sqrt{}\mathrm{3}\right)\left(\mathrm{1}+{i}\right)\left({cos}\theta−{isin}\theta\right) \\ $$
Answered by Ar Brandon last updated on 17/Sep/22
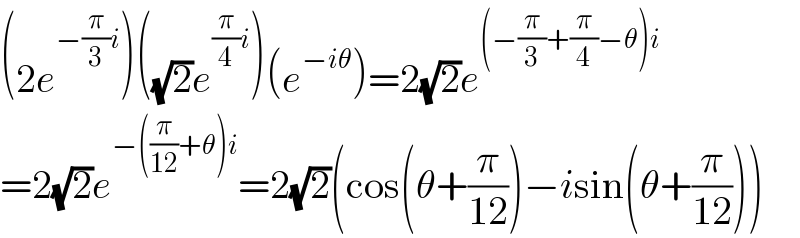
$$\left(\mathrm{2}{e}^{−\frac{\pi}{\mathrm{3}}{i}} \right)\left(\sqrt{\mathrm{2}}{e}^{\frac{\pi}{\mathrm{4}}{i}} \right)\left({e}^{−{i}\theta} \right)=\mathrm{2}\sqrt{\mathrm{2}}{e}^{\left(−\frac{\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{4}}−\theta\right){i}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}{e}^{−\left(\frac{\pi}{\mathrm{12}}+\theta\right){i}} =\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{cos}\left(\theta+\frac{\pi}{\mathrm{12}}\right)−{i}\mathrm{sin}\left(\theta+\frac{\pi}{\mathrm{12}}\right)\right) \\ $$
