
Question Number 176293 by mokys last updated on 15/Sep/22

$${find}\:{n}^{{th}} \:{formolla}\:{of}\:<\mathrm{0},\mathrm{4},\mathrm{9},\mathrm{16},\mathrm{25}> \\ $$
Answered by Frix last updated on 16/Sep/22
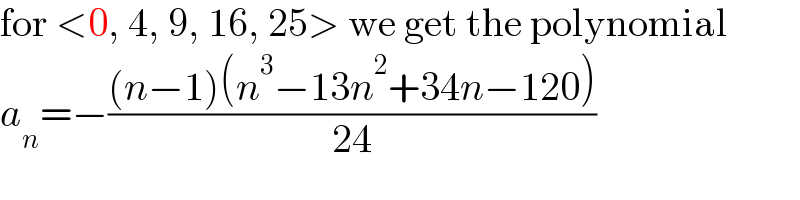
$$\mathrm{for}\:<\mathrm{0},\:\mathrm{4},\:\mathrm{9},\:\mathrm{16},\:\mathrm{25}>\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{polynomial} \\ $$ $${a}_{{n}} =−\frac{\left({n}−\mathrm{1}\right)\left({n}^{\mathrm{3}} −\mathrm{13}{n}^{\mathrm{2}} +\mathrm{34}{n}−\mathrm{120}\right)}{\mathrm{24}} \\ $$
Answered by Rasheed.Sindhi last updated on 16/Sep/22
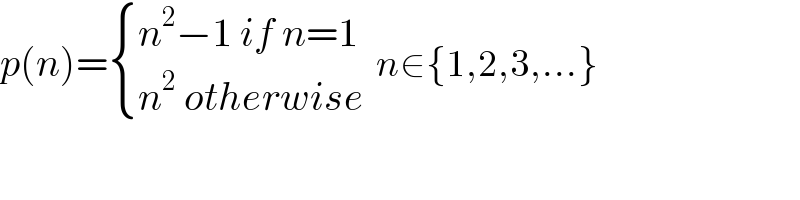
$${p}\left({n}\right)=\begin{cases}{{n}^{\mathrm{2}} −\mathrm{1}\:{if}\:{n}=\mathrm{1}}\\{{n}^{\mathrm{2}} \:{otherwise}}\end{cases}\:\:{n}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},...\right\} \\ $$
Answered by Rasheed.Sindhi last updated on 16/Sep/22

$$\:\:\:\:\:\:\bigstar\begin{array}{|c|}{\underset{\underset{\underset{\mathrm{0},\mathrm{4},\mathrm{9},\mathrm{16},\mathrm{25},...} {\boldsymbol{\mathcal{F}}\mathcal{OR}\:\mathcal{THE}\:\mathcal{SEQUENCE}}} {\boldsymbol{{of}}\:\boldsymbol{{nth}}\:\boldsymbol{{term}}}} {\mathbb{A}\:\mathbb{S}\boldsymbol{\mathrm{imple}}\:\mathbb{F}\boldsymbol{\mathrm{ormula}}}}\\\hline\end{array}\bigstar \\ $$ $$\begin{array}{|c|}{\:\:\begin{array}{|c|}{{a}_{{n}} ={n}^{\mathrm{2}} −\lfloor\frac{\mathrm{1}}{{n}}\rfloor\:\:;\:{n}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},...\right\}}\\\hline\end{array}_{} ^{} }\\\hline\end{array} \\ $$
Commented bymr W last updated on 16/Sep/22

$${or} \\ $$ $${a}_{{n}} ={sign}\left({n}−\mathrm{1}\right){n}^{\mathrm{2}} \\ $$
