
Question Number 176160 by peter frank last updated on 14/Sep/22
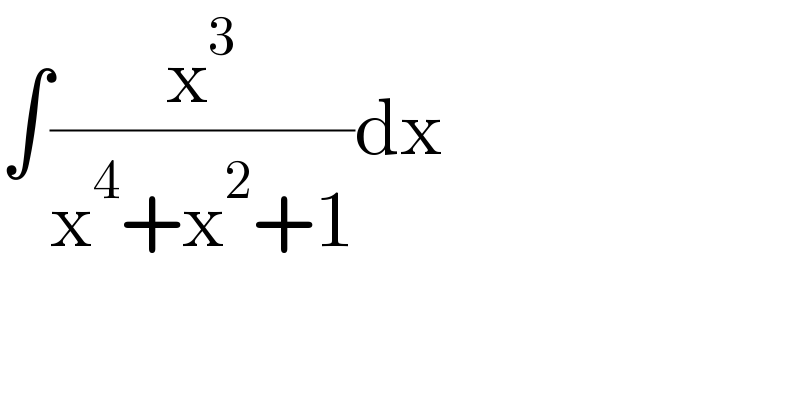
$$\int\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$
Answered by Ar Brandon last updated on 14/Sep/22
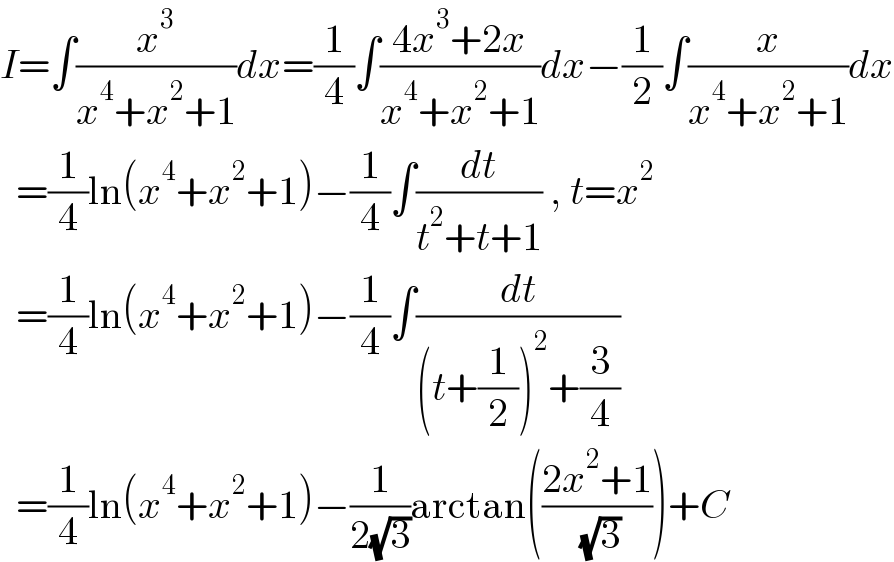
$${I}=\int\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{4}{x}^{\mathrm{3}} +\mathrm{2}{x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:,\:{t}={x}^{\mathrm{2}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+{C} \\ $$
Commented by peter frank last updated on 14/Sep/22
$$\mathrm{thank}\:\mathrm{you} \\ $$
