
Question Number 17614 by Tinkutara last updated on 08/Jul/17

$$\mathrm{The}\:\mathrm{triangle}\:\mathrm{ABC}\:\mathrm{has}\:\mathrm{CA}\:=\:\mathrm{CB}.\:\mathrm{P}\:\mathrm{is}\:\mathrm{a} \\ $$$$\mathrm{point}\:\mathrm{on}\:\mathrm{the}\:\mathrm{circumcircle}\:\mathrm{between}\:\mathrm{A} \\ $$$$\mathrm{and}\:\mathrm{B}\:\left(\mathrm{and}\:\mathrm{on}\:\mathrm{the}\:\mathrm{opposite}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the}\right. \\ $$$$\left.\mathrm{line}\:\mathrm{AB}\:\mathrm{to}\:\mathrm{C}\right).\:\mathrm{D}\:\mathrm{is}\:\mathrm{the}\:\mathrm{foot}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{perpendicular}\:\mathrm{from}\:\mathrm{C}\:\mathrm{to}\:\mathrm{PB}.\:\mathrm{Show}\:\mathrm{that} \\ $$$$\mathrm{PA}\:+\:\mathrm{PB}\:=\:\mathrm{2}\centerdot\mathrm{PD}. \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 08/Jul/17
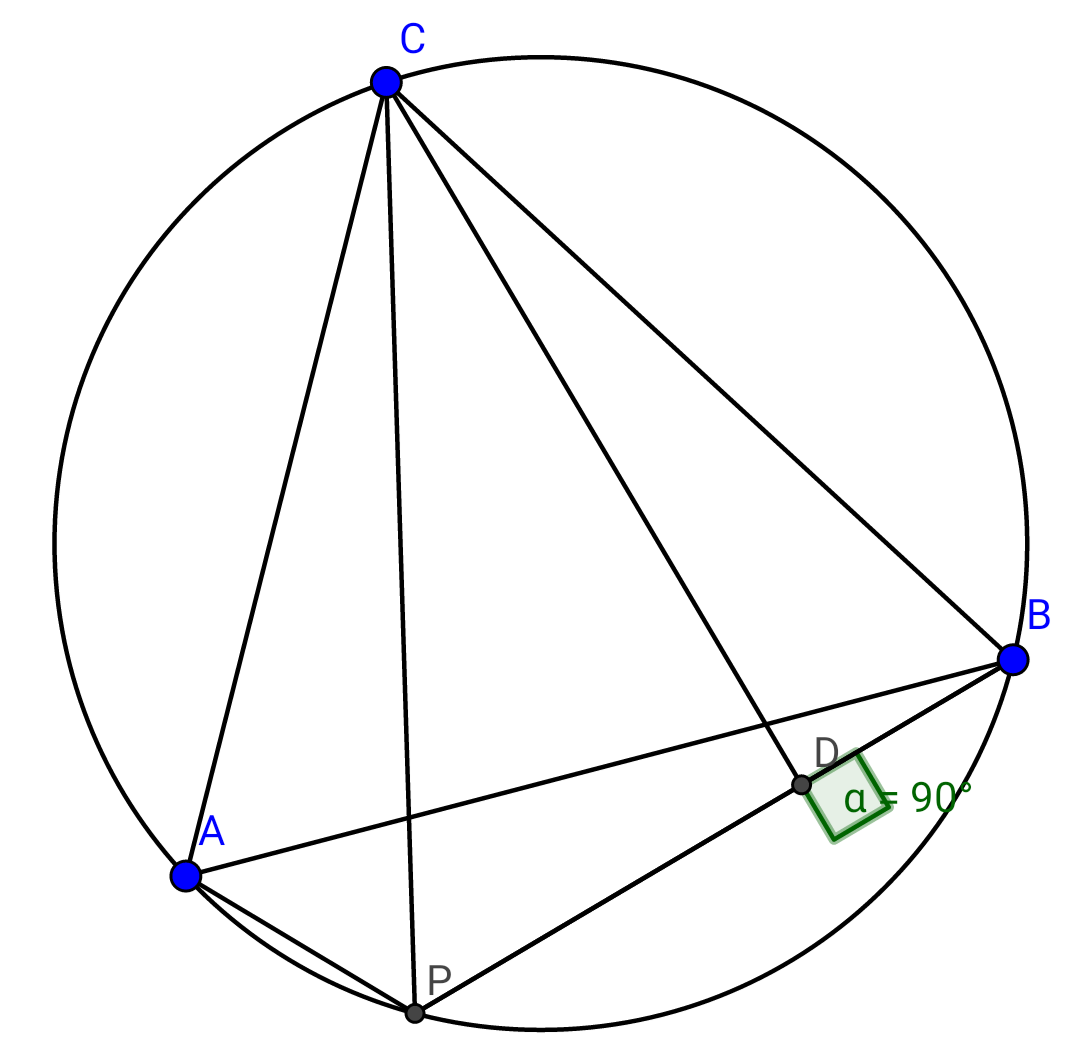
Commented by b.e.h.i.8.3.417@gmail.com last updated on 08/Jul/17

$${CA}×{PB}+{CB}×{PA}={CP}×{AB}\left({petolemy}'{s}\:{teorem}\right) \\ $$$$\Rightarrow{CA}\left({PA}+{PB}\right)={CP}×{AB} \\ $$$$\Rightarrow{PA}+{PB}=\frac{{CP}×{AB}}{{CA}} \\ $$$$\frac{{AB}}{{AC}}=\frac{{sinC}}{{sinB}}=\frac{{sin}\left(\mathrm{180}−\mathrm{2}{B}\right)}{{sinB}}=\frac{{sin}\mathrm{2}{B}}{{sinB}}=\mathrm{2}{cosB} \\ $$$${cos}\measuredangle{CPB}=\frac{{PD}}{{CP}}\Rightarrow{CP}=\frac{{PD}}{{cos}\measuredangle{CPB}}=\frac{{PD}}{{cosA}}= \\ $$$$=\frac{{PD}}{{cosB}} \\ $$$$\Rightarrow{PA}+{PB}=\frac{{CP}.{AB}}{{CA}}=\mathrm{2}{cosB}.\frac{{PD}}{{cosB}}=\mathrm{2}.{PD}\:.\blacksquare \\ $$$${note}:\measuredangle{CPB}=\measuredangle{CAB},\measuredangle{APC}=\measuredangle{ABC} \\ $$
Commented by Tinkutara last updated on 09/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
