
Question Number 176060 by doline last updated on 11/Sep/22

$${x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}=\mathrm{0} \\ $$
Answered by Ar Brandon last updated on 11/Sep/22
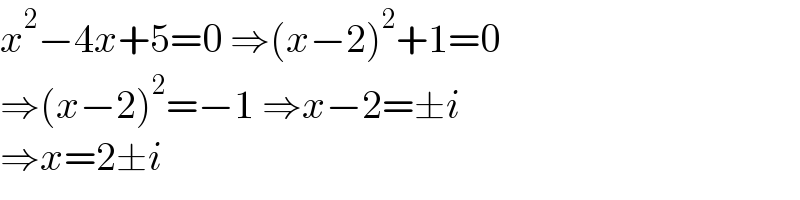
$${x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}=\mathrm{0}\:\Rightarrow\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{2}\right)^{\mathrm{2}} =−\mathrm{1}\:\Rightarrow{x}−\mathrm{2}=\pm{i} \\ $$$$\Rightarrow{x}=\mathrm{2}\pm{i} \\ $$
Answered by Devendra291999 last updated on 11/Sep/22

$$\mathrm{Solution} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{5}=\mathrm{0} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}×\mathrm{2x}+\mathrm{4}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} =−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{−\mathrm{1}=\mathrm{i}^{\mathrm{2}} \right\} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{i}^{\mathrm{2}} \\ $$$$\mathrm{x}−\mathrm{2}=\pm\mathrm{i} \\ $$$$\mathrm{x}=\mathrm{2}\pm\mathrm{iAnswer} \\ $$
