
Question Number 17599 by chux last updated on 08/Jul/17

$$\mathrm{a}\:\mathrm{particle}\:\mathrm{starts}\:\mathrm{with}\:\mathrm{an}\:\mathrm{initial} \\ $$$$\mathrm{speed}\:\mathrm{u},\mathrm{it}\:\mathrm{moves}\:\mathrm{in}\:\mathrm{a}\:\mathrm{straight} \\ $$$$\mathrm{line}\:\mathrm{with}\:\mathrm{an}\:\mathrm{accleration}\:\mathrm{which} \\ $$$$\mathrm{varies}\:\mathrm{as}\:\mathrm{the}\:\mathrm{square}\:\mathrm{of}\:\mathrm{the}\:\mathrm{time} \\ $$$$\mathrm{the}\:\mathrm{particle}\:\mathrm{has}\:\mathrm{been}\:\mathrm{in}\:\mathrm{motion}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{at}\:\mathrm{any}\:\mathrm{time}\:\mathrm{t},\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{distance}\:\mathrm{travelled}. \\ $$
Answered by Tinkutara last updated on 08/Jul/17
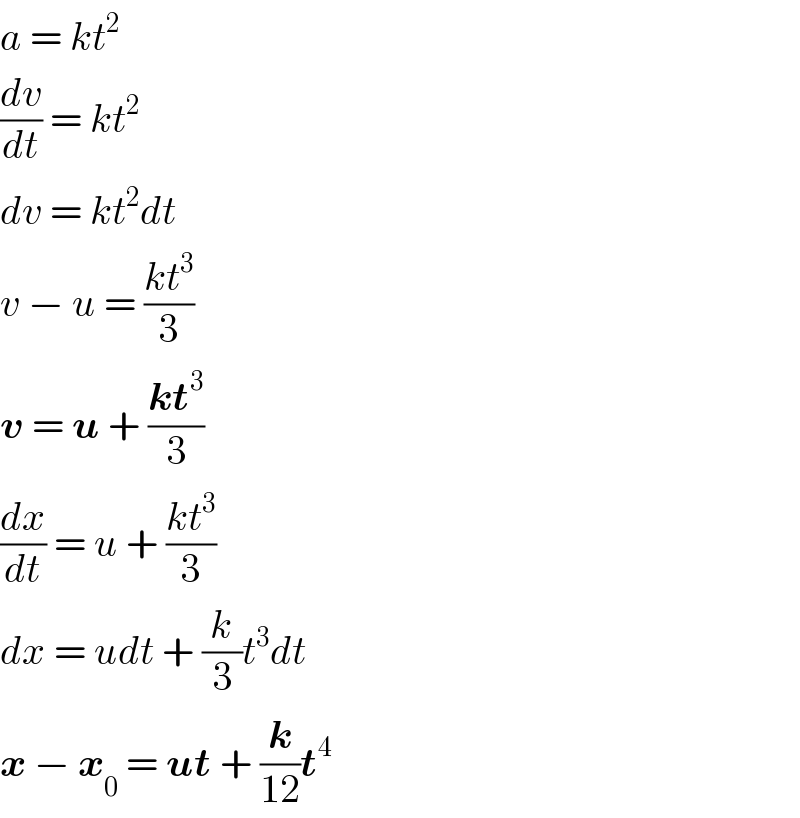
$${a}\:=\:{kt}^{\mathrm{2}} \\ $$$$\frac{{dv}}{{dt}}\:=\:{kt}^{\mathrm{2}} \\ $$$${dv}\:=\:{kt}^{\mathrm{2}} {dt} \\ $$$${v}\:−\:{u}\:=\:\frac{{kt}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\boldsymbol{{v}}\:=\:\boldsymbol{{u}}\:+\:\frac{\boldsymbol{{kt}}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\frac{{dx}}{{dt}}\:=\:{u}\:+\:\frac{{kt}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${dx}\:=\:{udt}\:+\:\frac{{k}}{\mathrm{3}}{t}^{\mathrm{3}} {dt} \\ $$$$\boldsymbol{{x}}\:−\:\boldsymbol{{x}}_{\mathrm{0}} \:=\:\boldsymbol{{ut}}\:+\:\frac{\boldsymbol{{k}}}{\mathrm{12}}\boldsymbol{{t}}^{\mathrm{4}} \\ $$
Commented by chux last updated on 08/Jul/17

$$\mathrm{wow}.....\:\mathrm{thankz} \\ $$
