
Question Number 175839 by Rasheed.Sindhi last updated on 08/Sep/22
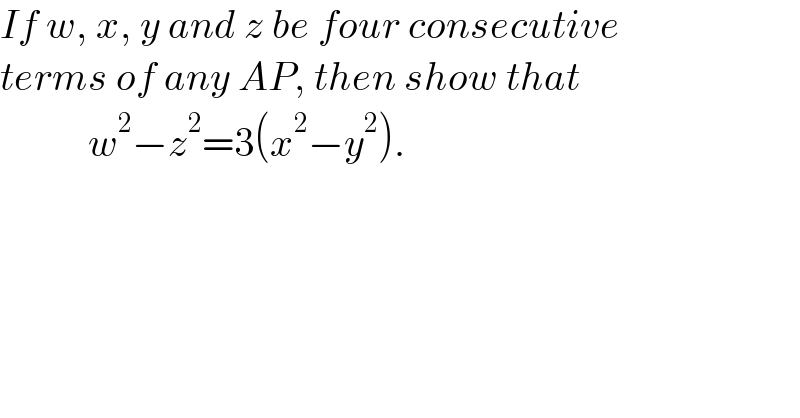
$${If}\:{w},\:{x},\:{y}\:{and}\:{z}\:{be}\:{four}\:{consecutive} \\ $$$${terms}\:{of}\:{any}\:{AP},\:{then}\:{show}\:{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{w}^{\mathrm{2}} −{z}^{\mathrm{2}} =\mathrm{3}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right). \\ $$
Answered by mr W last updated on 08/Sep/22

$${let}\:{c}=\frac{{x}+{y}}{\mathrm{2}},\:{d}={common}\:{difference} \\ $$$${w}={c}−\frac{\mathrm{3}{d}}{\mathrm{2}} \\ $$$${x}={c}−\frac{{d}}{\mathrm{2}} \\ $$$${y}={c}+\frac{{d}}{\mathrm{2}} \\ $$$${z}={c}+\frac{\mathrm{3}{d}}{\mathrm{2}} \\ $$$${w}^{\mathrm{2}} −{z}^{\mathrm{2}} =\left({c}−\frac{\mathrm{3}{d}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({c}+\frac{\mathrm{3}{d}}{\mathrm{2}}\right)^{\mathrm{2}} =−\mathrm{6}{cd} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\left({c}−\frac{{d}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({c}+\frac{{d}}{\mathrm{2}}\right)^{\mathrm{2}} =−\mathrm{2}{cd} \\ $$$$\Rightarrow{w}^{\mathrm{2}} −{z}^{\mathrm{2}} =\mathrm{3}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right) \\ $$
Commented by peter frank last updated on 08/Sep/22

$$\mathrm{thans} \\ $$
Commented by Rasheed.Sindhi last updated on 08/Sep/22

$$\mathbb{N}\mathrm{ice}\:\mathrm{sir},\:\mathrm{than}\Bbbk\mathrm{s}! \\ $$
Commented by Tawa11 last updated on 15/Sep/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Answered by Rasheed.Sindhi last updated on 08/Sep/22
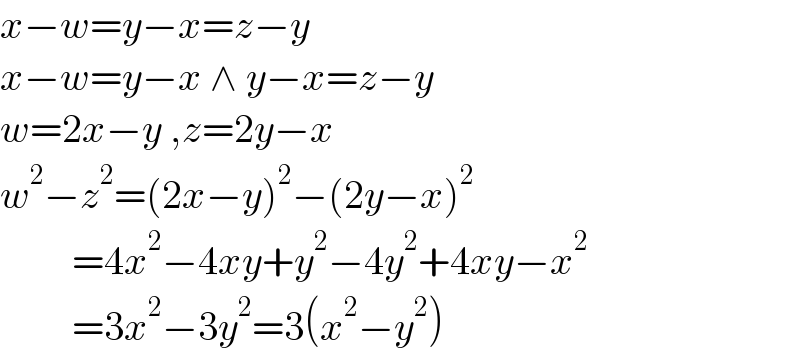
$${x}−{w}={y}−{x}={z}−{y} \\ $$$${x}−{w}={y}−{x}\:\wedge\:{y}−{x}={z}−{y} \\ $$$${w}=\mathrm{2}{x}−{y}\:,{z}=\mathrm{2}{y}−{x} \\ $$$${w}^{\mathrm{2}} −{z}^{\mathrm{2}} =\left(\mathrm{2}{x}−{y}\right)^{\mathrm{2}} −\left(\mathrm{2}{y}−{x}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{xy}+{y}^{\mathrm{2}} −\mathrm{4}{y}^{\mathrm{2}} +\mathrm{4}{xy}−{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} =\mathrm{3}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right) \\ $$
