
Question Number 17580 by b.e.h.i.8.3.417@gmail.com last updated on 08/Jul/17
Commented by b.e.h.i.8.3.417@gmail.com last updated on 08/Jul/17

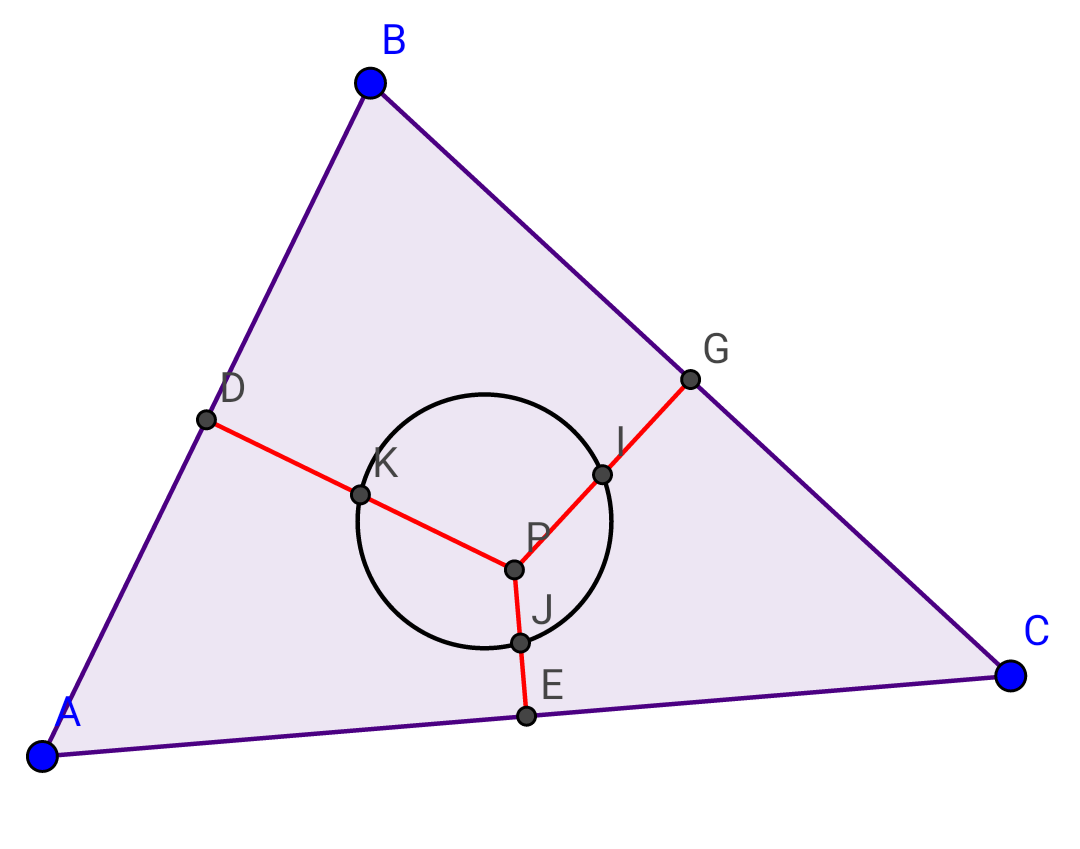
$${triangle}\:{ABC},{is}\:{given}\:{with}: \\ $$$${AB}={c},{BC}={a},{AC}={b} \\ $$$${red}\:\:{lines},{are}\:{perpendicular}\:{bisectors} \\ $$$${of}\:{sides}. \\ $$$$\left.\mathrm{1}\right){find}\:{radius}\:{of}\:{a}\:{circle}\:{that}\:{passes} \\ $$$${trough}\:{midpoints}\:{of}\:{red}\:\:{lines}. \\ $$$$\left.\mathrm{2}\right){if}\:'{Z}',{be}\:{the}\:{center}\:{of}\:{this}\:{circle}, \\ $$$${find}:\:\:{PZ}\:\left({in}\:{terms}\:{of}:\:{a},{b},{c}\right) \\ $$$${trial}\:{case}: \\ $$$${a}=\mathrm{15}.\mathrm{93},{b}=\mathrm{15}.\mathrm{76},{c}=\mathrm{12}.\mathrm{51} \\ $$$$\Rightarrow{r}=\mathrm{2}.\mathrm{16}\:\:\:\:,{PZ}=\mathrm{0}.\mathrm{81}\:. \\ $$
Commented by mrW1 last updated on 08/Jul/17
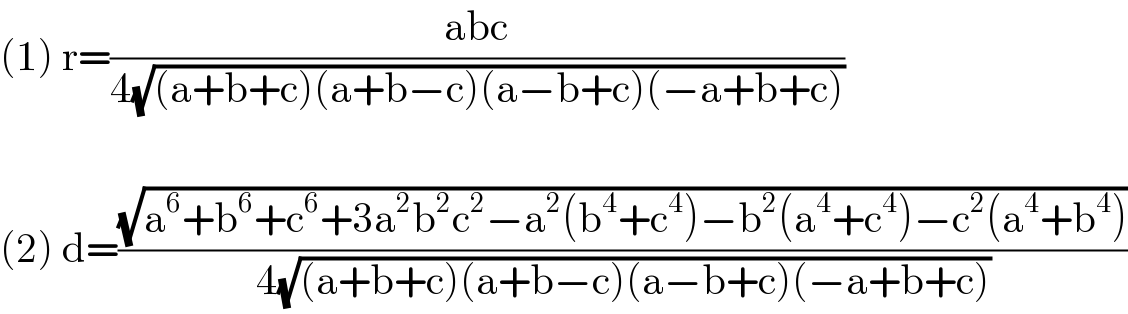
$$\left(\mathrm{1}\right)\:\mathrm{r}=\frac{\mathrm{abc}}{\mathrm{4}\sqrt{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)}} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\mathrm{d}=\frac{\sqrt{\mathrm{a}^{\mathrm{6}} +\mathrm{b}^{\mathrm{6}} +\mathrm{c}^{\mathrm{6}} +\mathrm{3a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \left(\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \right)−\mathrm{b}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \right)−\mathrm{c}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} \right)}}{\mathrm{4}\sqrt{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)}} \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 08/Jul/17

$${very}\:{right}\:{answers}.{beautiful}\:{relations}. \\ $$$${thank}\:{you}\:{master}. \\ $$$${please}\:{post}\:{the}\:{solution},{if}\:{it}\:{possible}. \\ $$
Commented by mrW1 last updated on 09/Jul/17
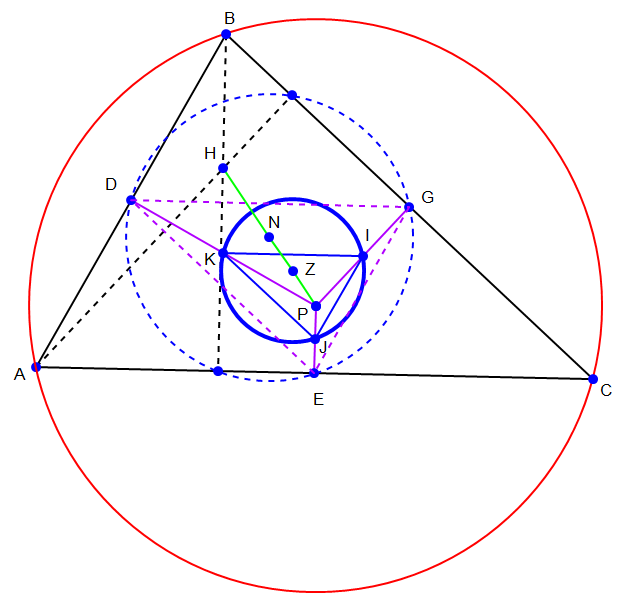
![Part 1: ΔDGE∼ΔACB with side length ratio 1:2 ΔKIJ∼ΔDGE with side length ratio 1:2 ⇒ΔKIJ∼ΔACB with side length ratio 1:4 let r=radius of circumcircle of ΔKIJ let R=radius of circumcircle of ΔABC ⇒r=(1/4)R R=PA=PB=PC diameter of circumcircle of ΔABC=((abc)/(2 A_(ΔABC) )) R=((abc)/(4 A_(ΔABC) ))=((abc)/(4(√(s(s−a)(s−b)(s−c))))) =((abc)/(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))) ⇒r=(1/4)R=((abc)/(4(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c))))) Part 2: let x=distance between orthocenter (H) and circumcenter (P) x^2 =9R^2 −(a^2 +b^2 +c^2 ) =((9a^2 b^2 c^2 )/((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))−(a^2 +b^2 +c^2 ) =((9a^2 b^2 c^2 −[(a+b)+c][(a+b)−c][c+(a−b)][c−(a−b)](a^2 +b^2 +c^2 ))/((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) =((9a^2 b^2 c^2 −[(a+b)^2 −c^2 ][c^2 −(a−b)^2 ](a^2 +b^2 +c^2 ))/((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) =((9a^2 b^2 c^2 +[a^2 +b^2 −c^2 +2ab][a^2 +b^2 −c^2 −2ab](a^2 +b^2 +c^2 ))/((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) =((9a^2 b^2 c^2 +[(a^2 +b^2 −c^2 )^2 −4a^2 b^2 ](a^2 +b^2 +c^2 ))/((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) =((a^2 b^2 (−4a^2 −4b^2 +5c^2 )+(a^2 +b^2 −c^2 )^2 (a^2 +b^2 +c^2 ))/((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) =((a^2 b^2 (−4a^2 −4b^2 +5c^2 )+(a^2 +b^2 −c^2 )[(a^2 +b^2 )^2 −c^4 ])/((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) =((a^2 b^2 (−4a^2 −4b^2 +5c^2 )+(a^2 +b^2 −c^2 )[a^4 +b^4 −c^4 +2a^2 b^2 ])/((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) =(((−4a^4 b^2 −4a^2 b^4 +5a^2 b^2 c^2 )+(a^6 +a^2 b^4 −a^2 c^4 +2a^4 b^2 +b^2 a^4 +b^6 −b^2 c^4 +2a^2 b^4 −c^2 a^4 −c^2 b^4 +c^6 −2a^2 b^2 c^2 ))/((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) =((a^6 +b^6 +c^6 +3a^2 b^2 c^2 −a^4 (b^2 +c^2 )−b^4 (a^2 +c^2 )−c^4 (a^2 +b^2 ))/((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) ⇒x=(√((a^6 +b^6 +c^6 +3a^2 b^2 c^2 −a^4 (b^2 +c^2 )−b^4 (a^2 +c^2 )−c^4 (a^2 +b^2 ))/((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))) distance between nine−point−circle center (N) and circumcenter (P) =(x/2) since circle Z is half as large as circle N, point Z is midpoint between nine−point−circle center and circumcenter ⇒d=(x/4)=((√(a^6 +b^6 +c^6 +3a^2 b^2 c^2 −a^4 (b^2 +c^2 )−b^4 (a^2 +c^2 )−c^4 (a^2 +b^2 )))/(4(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))))](Q17632.png)
$$\mathrm{Part}\:\mathrm{1}: \\ $$$$ \\ $$$$\Delta\mathrm{DGE}\sim\Delta\mathrm{ACB}\:\mathrm{with}\:\mathrm{side}\:\mathrm{length}\:\mathrm{ratio}\:\mathrm{1}:\mathrm{2} \\ $$$$\Delta\mathrm{KIJ}\sim\Delta\mathrm{DGE}\:\mathrm{with}\:\mathrm{side}\:\mathrm{length}\:\mathrm{ratio}\:\mathrm{1}:\mathrm{2} \\ $$$$\Rightarrow\Delta\mathrm{KIJ}\sim\Delta\mathrm{ACB}\:\mathrm{with}\:\mathrm{side}\:\mathrm{length}\:\mathrm{ratio}\:\mathrm{1}:\mathrm{4} \\ $$$$\mathrm{let}\:\mathrm{r}=\mathrm{radius}\:\mathrm{of}\:\mathrm{circumcircle}\:\mathrm{of}\:\Delta\mathrm{KIJ} \\ $$$$\mathrm{let}\:\mathrm{R}=\mathrm{radius}\:\mathrm{of}\:\mathrm{circumcircle}\:\mathrm{of}\:\Delta\mathrm{ABC} \\ $$$$\Rightarrow\mathrm{r}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{R} \\ $$$$ \\ $$$$\mathrm{R}=\mathrm{PA}=\mathrm{PB}=\mathrm{PC} \\ $$$$\mathrm{diameter}\:\mathrm{of}\:\mathrm{circumcircle}\:\mathrm{of}\:\Delta\mathrm{ABC}=\frac{\mathrm{abc}}{\mathrm{2}\:\mathrm{A}_{\Delta\mathrm{ABC}} } \\ $$$$\mathrm{R}=\frac{\mathrm{abc}}{\mathrm{4}\:\mathrm{A}_{\Delta\mathrm{ABC}} }=\frac{\mathrm{abc}}{\mathrm{4}\sqrt{\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)}} \\ $$$$=\frac{\mathrm{abc}}{\sqrt{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)}} \\ $$$$ \\ $$$$\Rightarrow\mathrm{r}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{R}=\frac{\mathrm{abc}}{\mathrm{4}\sqrt{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)}} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Part}\:\mathrm{2}:\: \\ $$$$\mathrm{let}\:\mathrm{x}=\mathrm{distance}\:\mathrm{between}\:\mathrm{orthocenter}\:\left(\mathrm{H}\right)\:\mathrm{and}\:\mathrm{circumcenter}\:\left(\mathrm{P}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{9R}^{\mathrm{2}} −\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{9a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} }{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)}−\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{9a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\left[\left(\mathrm{a}+\mathrm{b}\right)+\mathrm{c}\right]\left[\left(\mathrm{a}+\mathrm{b}\right)−\mathrm{c}\right]\left[\mathrm{c}+\left(\mathrm{a}−\mathrm{b}\right)\right]\left[\mathrm{c}−\left(\mathrm{a}−\mathrm{b}\right)\right]\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)} \\ $$$$=\frac{\mathrm{9a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\left[\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right]\left[\mathrm{c}^{\mathrm{2}} −\left(\mathrm{a}−\mathrm{b}\right)^{\mathrm{2}} \right]\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)} \\ $$$$=\frac{\mathrm{9a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\left[\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} +\mathrm{2ab}\right]\left[\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} −\mathrm{2ab}\right]\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)} \\ $$$$=\frac{\mathrm{9a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\left[\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \right]\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)} \\ $$$$=\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \left(−\mathrm{4a}^{\mathrm{2}} −\mathrm{4b}^{\mathrm{2}} +\mathrm{5c}^{\mathrm{2}} \right)+\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)} \\ $$$$=\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \left(−\mathrm{4a}^{\mathrm{2}} −\mathrm{4b}^{\mathrm{2}} +\mathrm{5c}^{\mathrm{2}} \right)+\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)\left[\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{c}^{\mathrm{4}} \right]}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)} \\ $$$$=\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \left(−\mathrm{4a}^{\mathrm{2}} −\mathrm{4b}^{\mathrm{2}} +\mathrm{5c}^{\mathrm{2}} \right)+\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)\left[\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} −\mathrm{c}^{\mathrm{4}} +\mathrm{2a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \right]}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)} \\ $$$$=\frac{\left(−\mathrm{4a}^{\mathrm{4}} \mathrm{b}^{\mathrm{2}} −\mathrm{4a}^{\mathrm{2}} \mathrm{b}^{\mathrm{4}} +\mathrm{5a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} \right)+\left(\mathrm{a}^{\mathrm{6}} +\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{4}} −\mathrm{a}^{\mathrm{2}} \mathrm{c}^{\mathrm{4}} +\mathrm{2a}^{\mathrm{4}} \mathrm{b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{6}} −\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{4}} +\mathrm{2a}^{\mathrm{2}} \mathrm{b}^{\mathrm{4}} −\mathrm{c}^{\mathrm{2}} \mathrm{a}^{\mathrm{4}} −\mathrm{c}^{\mathrm{2}} \mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{6}} −\mathrm{2a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} \right)}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)} \\ $$$$=\frac{\mathrm{a}^{\mathrm{6}} +\mathrm{b}^{\mathrm{6}} +\mathrm{c}^{\mathrm{6}} +\mathrm{3a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{4}} \left(\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)−\mathrm{b}^{\mathrm{4}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)−\mathrm{c}^{\mathrm{4}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)} \\ $$$$\Rightarrow\mathrm{x}=\sqrt{\frac{\mathrm{a}^{\mathrm{6}} +\mathrm{b}^{\mathrm{6}} +\mathrm{c}^{\mathrm{6}} +\mathrm{3a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{4}} \left(\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)−\mathrm{b}^{\mathrm{4}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)−\mathrm{c}^{\mathrm{4}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)}} \\ $$$$ \\ $$$$\mathrm{distance}\:\mathrm{between}\:\mathrm{nine}−\mathrm{point}−\mathrm{circle}\:\mathrm{center}\:\left(\mathrm{N}\right)\:\mathrm{and}\:\mathrm{circumcenter}\:\left(\mathrm{P}\right) \\ $$$$=\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{since}\:\mathrm{circle}\:\mathrm{Z}\:\mathrm{is}\:\mathrm{half}\:\mathrm{as}\:\mathrm{large}\:\mathrm{as}\:\mathrm{circle}\:\mathrm{N}, \\ $$$$\mathrm{point}\:\mathrm{Z}\:\mathrm{is}\:\mathrm{midpoint}\:\mathrm{between}\:\mathrm{nine}−\mathrm{point}−\mathrm{circle}\:\mathrm{center}\:\:\mathrm{and}\:\mathrm{circumcenter} \\ $$$$\Rightarrow\mathrm{d}=\frac{\mathrm{x}}{\mathrm{4}}=\frac{\sqrt{\mathrm{a}^{\mathrm{6}} +\mathrm{b}^{\mathrm{6}} +\mathrm{c}^{\mathrm{6}} +\mathrm{3a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{4}} \left(\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)−\mathrm{b}^{\mathrm{4}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)−\mathrm{c}^{\mathrm{4}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}}{\mathrm{4}\sqrt{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(−\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)}} \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 08/Jul/17
$${thanks}\:{master}.{i}\:{am}\:{waiting}\:{for}\:{part}\mathrm{2}.... \\ $$
Commented by mrW1 last updated on 09/Jul/17
Commented by b.e.h.i.8.3.417@gmail.com last updated on 09/Jul/17

$${waiting}\:{is}\:{over}. \\ $$$${thank}\:{you}\:{very}\:{much}\:{dear}\:{master}. \\ $$$${so}\:{beautiful}\:{and}\:{smart}. \\ $$$${god}\:{blees}\:{you}\:{sir}.{thanks}\:{a}\:{lot}\:{again}. \\ $$
Commented by mrW1 last updated on 09/Jul/17
$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome}\:\mathrm{sir}! \\ $$
