
Question Number 175740 by daus last updated on 06/Sep/22
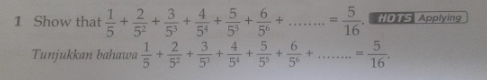
Answered by Ar Brandon last updated on 06/Sep/22
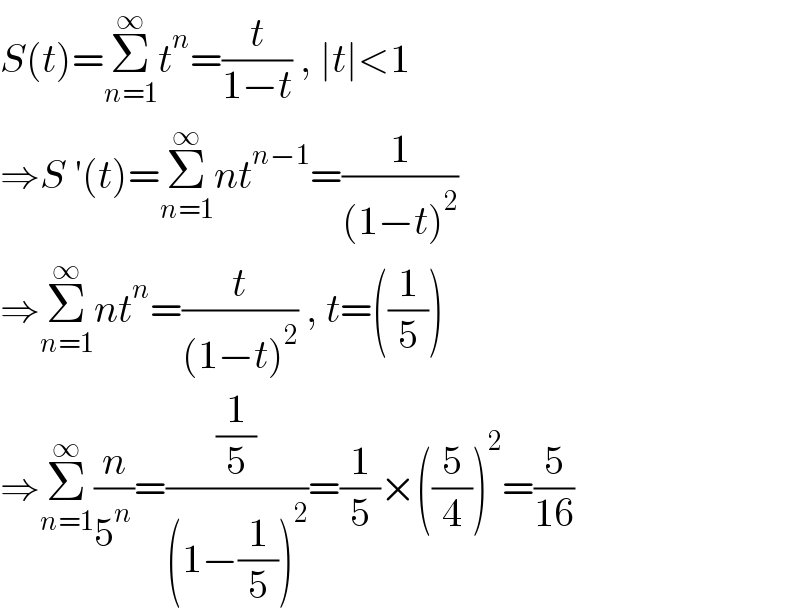
$${S}\left({t}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{t}^{{n}} =\frac{{t}}{\mathrm{1}−{t}}\:,\:\mid{t}\mid<\mathrm{1} \\ $$$$\Rightarrow{S}\:'\left({t}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nt}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nt}^{{n}} =\frac{{t}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }\:,\:{t}=\left(\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{\mathrm{5}^{{n}} }=\frac{\frac{\mathrm{1}}{\mathrm{5}}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{5}}×\left(\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{16}} \\ $$
Answered by Ar Brandon last updated on 06/Sep/22
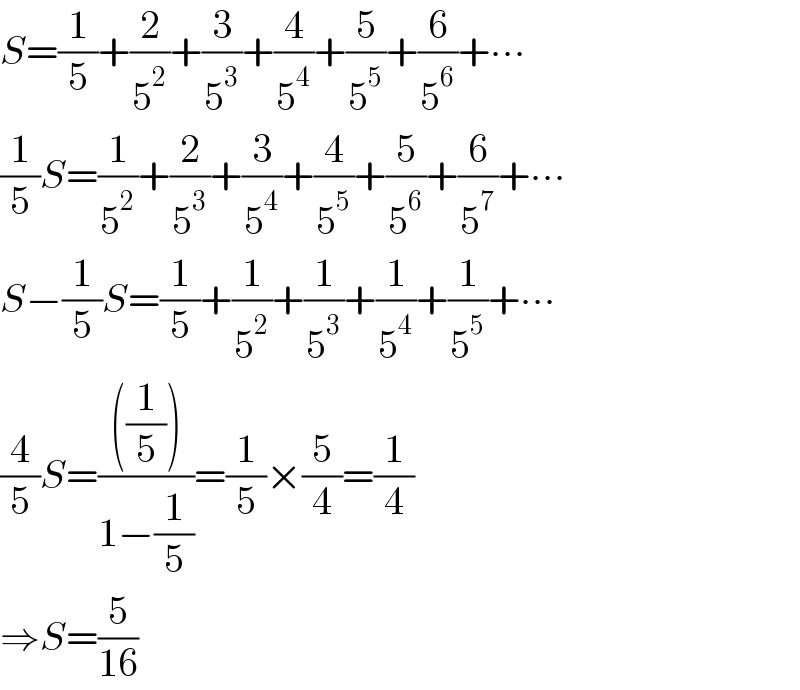
$${S}=\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{5}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{5}^{\mathrm{4}} }+\frac{\mathrm{5}}{\mathrm{5}^{\mathrm{5}} }+\frac{\mathrm{6}}{\mathrm{5}^{\mathrm{6}} }+\centerdot\centerdot\centerdot \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}{S}=\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{5}^{\mathrm{3}} }+\frac{\mathrm{3}}{\mathrm{5}^{\mathrm{4}} }+\frac{\mathrm{4}}{\mathrm{5}^{\mathrm{5}} }+\frac{\mathrm{5}}{\mathrm{5}^{\mathrm{6}} }+\frac{\mathrm{6}}{\mathrm{5}^{\mathrm{7}} }+\centerdot\centerdot\centerdot \\ $$$${S}−\frac{\mathrm{1}}{\mathrm{5}}{S}=\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{5}} }+\centerdot\centerdot\centerdot \\ $$$$\frac{\mathrm{4}}{\mathrm{5}}{S}=\frac{\left(\frac{\mathrm{1}}{\mathrm{5}}\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}}=\frac{\mathrm{1}}{\mathrm{5}}×\frac{\mathrm{5}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{S}=\frac{\mathrm{5}}{\mathrm{16}} \\ $$
Commented by daus last updated on 07/Sep/22
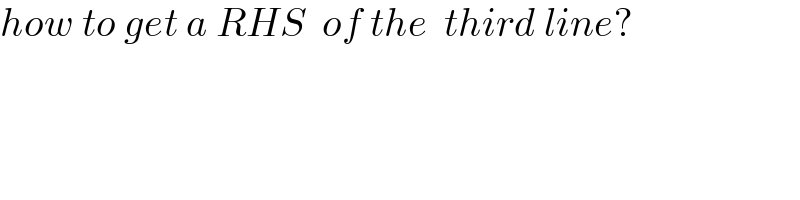
$${how}\:{to}\:{get}\:{a}\:{RHS}\:\:{of}\:{the}\:\:{third}\:{line}? \\ $$
Commented by Ar Brandon last updated on 07/Sep/22
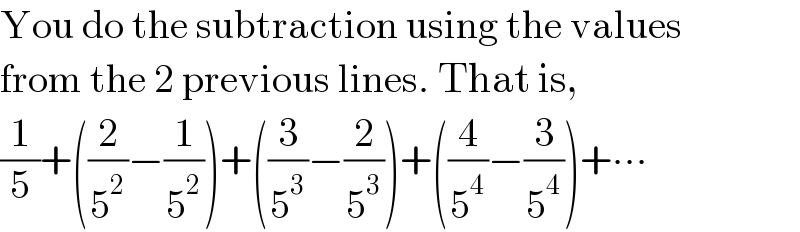
$$\mathrm{You}\:\mathrm{do}\:\mathrm{the}\:\mathrm{subtraction}\:\mathrm{using}\:\mathrm{the}\:\mathrm{values} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{2}\:\mathrm{previous}\:\mathrm{lines}.\:\mathrm{That}\:\mathrm{is}, \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}+\left(\frac{\mathrm{2}}{\mathrm{5}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }\right)+\left(\frac{\mathrm{3}}{\mathrm{5}^{\mathrm{3}} }−\frac{\mathrm{2}}{\mathrm{5}^{\mathrm{3}} }\right)+\left(\frac{\mathrm{4}}{\mathrm{5}^{\mathrm{4}} }−\frac{\mathrm{3}}{\mathrm{5}^{\mathrm{4}} }\right)+\centerdot\centerdot\centerdot \\ $$
Commented by peter frank last updated on 06/Sep/22

$$\mathrm{thanks} \\ $$
Commented by Tawa11 last updated on 15/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 06/Sep/22
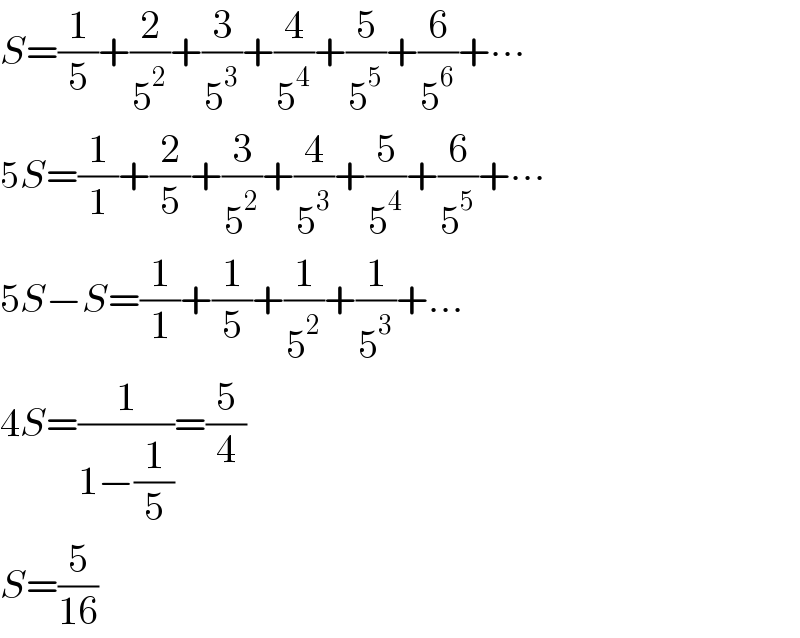
$${S}=\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{5}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{5}^{\mathrm{4}} }+\frac{\mathrm{5}}{\mathrm{5}^{\mathrm{5}} }+\frac{\mathrm{6}}{\mathrm{5}^{\mathrm{6}} }+\centerdot\centerdot\centerdot \\ $$$$\mathrm{5}{S}=\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{3}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{5}^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{5}^{\mathrm{4}} }+\frac{\mathrm{6}}{\mathrm{5}^{\mathrm{5}} }+\centerdot\centerdot\centerdot \\ $$$$\mathrm{5}{S}−{S}=\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{3}} }+... \\ $$$$\mathrm{4}{S}=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${S}=\frac{\mathrm{5}}{\mathrm{16}} \\ $$
Commented by peter frank last updated on 06/Sep/22

$$\mathrm{thanks} \\ $$
