Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 175593 by Shrinava last updated on 03/Sep/22

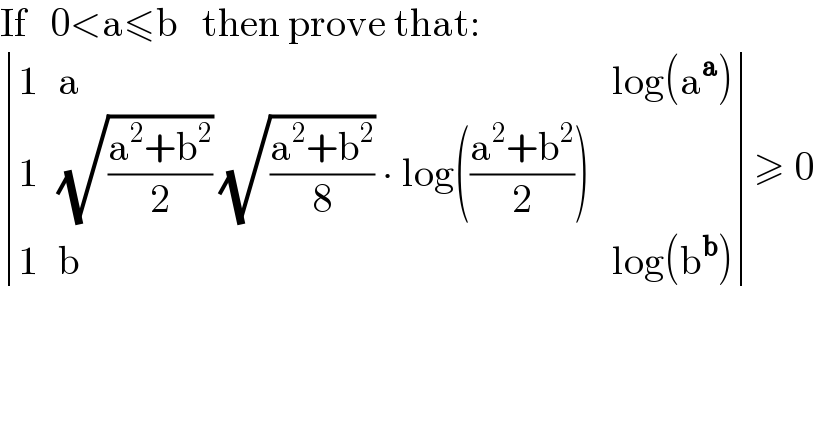
If 0<a≤b then prove that: determinant ((1,a,(log(a^a ))),(1,((√((a^2 +b^2 )/2)) (√((a^2 +b^2 )/8)) ∙ log(((a^2 +b^2 )/2))),),(1,b,(log(b^b ))))≥ 0

$$\mathrm{If}\:\:\:\mathrm{0}<\mathrm{a}\leqslant\mathrm{b}\:\:\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that}: \\ $$ $$\begin{vmatrix}{\mathrm{1}}&{\mathrm{a}}&{\mathrm{log}\left(\mathrm{a}^{\boldsymbol{\mathrm{a}}} \right)}\\{\mathrm{1}}&{\sqrt{\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}}\:\sqrt{\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{8}}}\:\centerdot\:\mathrm{log}\left(\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}\right)}&{}\\{\mathrm{1}}&{\mathrm{b}}&{\mathrm{log}\left(\mathrm{b}^{\boldsymbol{\mathrm{b}}} \right)}\end{vmatrix}\geqslant\:\mathrm{0} \\ $$

Commented byRasheed.Sindhi last updated on 03/Sep/22

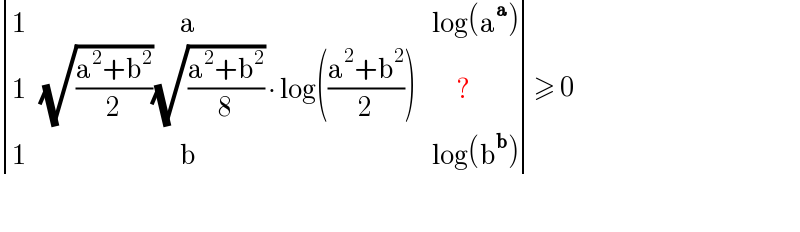
determinant ((1,( a),(log(a^a ))),(1,((√((a^2 +b^2 )/2))(√((a^2 +b^2 )/8)) ∙ log(((a^2 +b^2 )/2))),( ?)),(1,( b),(log(b^b ))))≥ 0

$$\begin{vmatrix}{\mathrm{1}}&{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}}&{\mathrm{log}\left(\mathrm{a}^{\boldsymbol{\mathrm{a}}} \right)}\\{\mathrm{1}}&{\sqrt{\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}}\sqrt{\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{8}}}\:\centerdot\:\mathrm{log}\left(\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}\right)}&{\:\:\:\:\:\:?}\\{\mathrm{1}}&{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{b}}&{\mathrm{log}\left(\mathrm{b}^{\boldsymbol{\mathrm{b}}} \right)}\end{vmatrix}\geqslant\:\mathrm{0} \\ $$ $$ \\ $$

Commented byJDamian last updated on 03/Sep/22

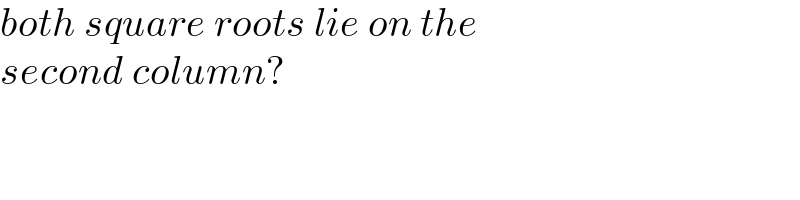
both square roots lie on the second column?

$${both}\:{square}\:{roots}\:{lie}\:{on}\:{the} \\ $$ $${second}\:{column}? \\ $$

Commented byShrinava last updated on 03/Sep/22

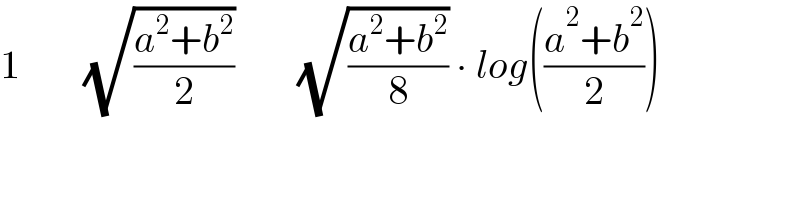
1 (√((a^2 +b^2 )/2)) (√((a^2 +b^2 )/8)) ∙ log(((a^2 +b^2 )/2))

$$\mathrm{1}\:\:\:\:\:\:\:\:\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}}}\:\:\:\:\:\:\:\:\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{8}}}\:\centerdot\:{log}\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com