
Question Number 175407 by Stephan last updated on 29/Aug/22

$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\underline{\mathrm{Trouver}\:\mathrm{la}\:\mathrm{somme}\:\mathrm{de}\:\mathrm{S}_{{n}} }\:\: \\ $$$$\:\:\:\mathrm{Si}\:\:\:\:\:\:{S}_{{n}} =\mathrm{1}+\mathrm{11}+\mathrm{111}+...+\mathrm{1111}...\mathrm{111}\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 29/Aug/22
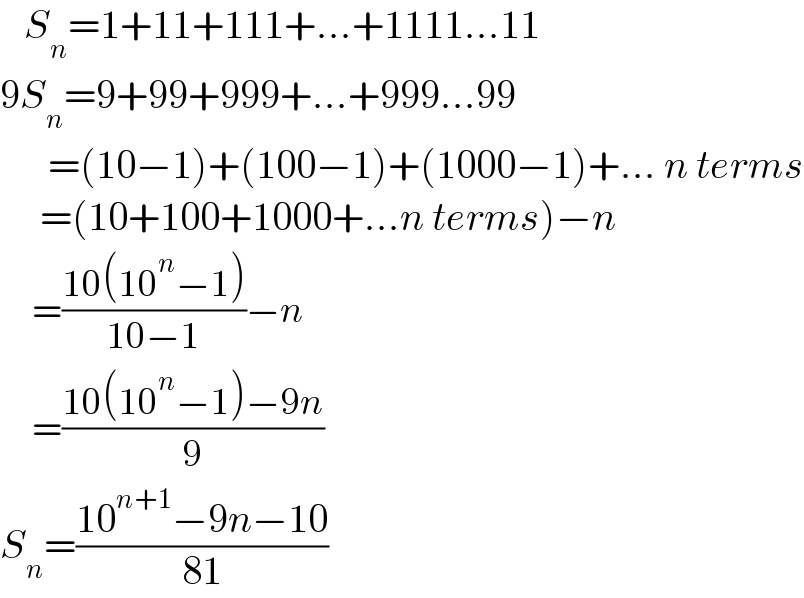
$$\:\:\:{S}_{{n}} =\mathrm{1}+\mathrm{11}+\mathrm{111}+...+\mathrm{1111}...\mathrm{11} \\ $$$$\mathrm{9}{S}_{{n}} =\mathrm{9}+\mathrm{99}+\mathrm{999}+...+\mathrm{999}...\mathrm{99} \\ $$$$\:\:\:\:\:\:=\left(\mathrm{10}−\mathrm{1}\right)+\left(\mathrm{100}−\mathrm{1}\right)+\left(\mathrm{1000}−\mathrm{1}\right)+...\:{n}\:{terms} \\ $$$$\:\:\:\:\:=\left(\mathrm{10}+\mathrm{100}+\mathrm{1000}+...{n}\:{terms}\right)−{n} \\ $$$$\:\:\:\:\:=\frac{\mathrm{10}\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{10}−\mathrm{1}}−{n}\:\:\:\: \\ $$$$\:\:\:\:\:=\frac{\mathrm{10}\left(\mathrm{10}^{{n}} −\mathrm{1}\right)−\mathrm{9}{n}}{\mathrm{9}} \\ $$$${S}_{{n}} =\frac{\mathrm{10}^{{n}+\mathrm{1}} −\mathrm{9}{n}−\mathrm{10}}{\mathrm{81}}\:\:\:\: \\ $$
Answered by Ar Brandon last updated on 29/Aug/22
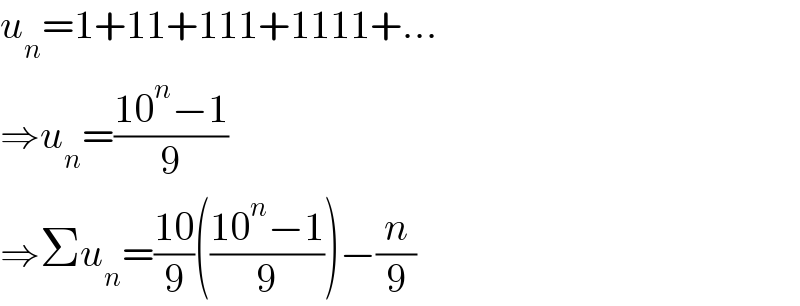
$${u}_{{n}} =\mathrm{1}+\mathrm{11}+\mathrm{111}+\mathrm{1111}+... \\ $$$$\Rightarrow{u}_{{n}} =\frac{\mathrm{10}^{{n}} −\mathrm{1}}{\mathrm{9}} \\ $$$$\Rightarrow\Sigma{u}_{{n}} =\frac{\mathrm{10}}{\mathrm{9}}\left(\frac{\mathrm{10}^{{n}} −\mathrm{1}}{\mathrm{9}}\right)−\frac{{n}}{\mathrm{9}} \\ $$
