
Question Number 175042 by peter frank last updated on 17/Aug/22
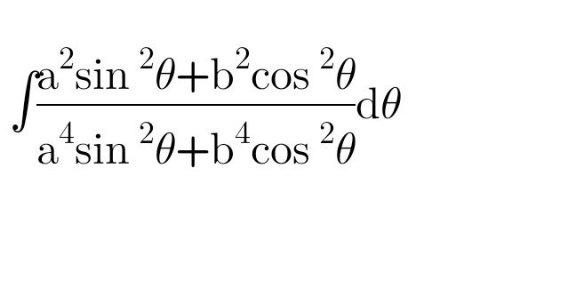
Answered by Frix last updated on 18/Aug/22
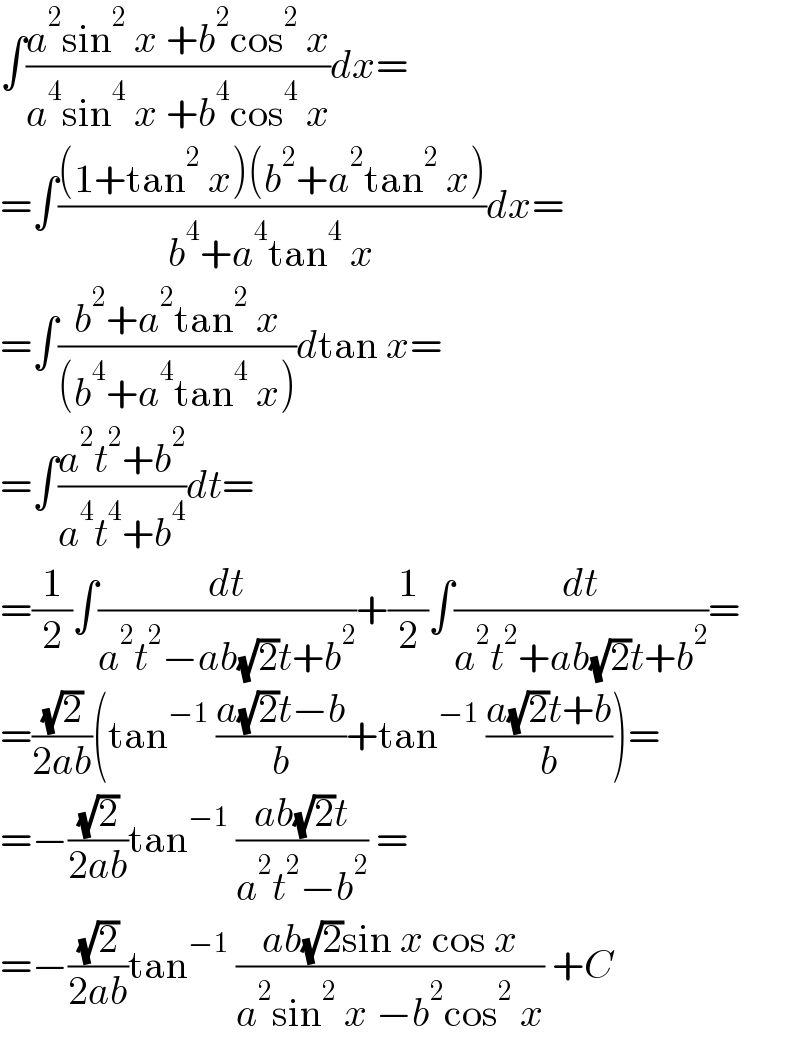
$$\int\frac{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:{x}\:+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:{x}}{{a}^{\mathrm{4}} \mathrm{sin}^{\mathrm{4}} \:{x}\:+{b}^{\mathrm{4}} \mathrm{cos}^{\mathrm{4}} \:{x}}{dx}= \\ $$$$=\int\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}\right)\left({b}^{\mathrm{2}} +{a}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:{x}\right)}{{b}^{\mathrm{4}} +{a}^{\mathrm{4}} \mathrm{tan}^{\mathrm{4}} \:{x}}{dx}= \\ $$$$=\int\frac{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:{x}}{\left({b}^{\mathrm{4}} +{a}^{\mathrm{4}} \mathrm{tan}^{\mathrm{4}} \:{x}\right)}{d}\mathrm{tan}\:{x}= \\ $$$$=\int\frac{{a}^{\mathrm{2}} {t}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{a}^{\mathrm{4}} {t}^{\mathrm{4}} +{b}^{\mathrm{4}} }{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{a}^{\mathrm{2}} {t}^{\mathrm{2}} −{ab}\sqrt{\mathrm{2}}{t}+{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{a}^{\mathrm{2}} {t}^{\mathrm{2}} +{ab}\sqrt{\mathrm{2}}{t}+{b}^{\mathrm{2}} }= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}{ab}}\left(\mathrm{tan}^{−\mathrm{1}} \:\frac{{a}\sqrt{\mathrm{2}}{t}−{b}}{{b}}+\mathrm{tan}^{−\mathrm{1}} \:\frac{{a}\sqrt{\mathrm{2}}{t}+{b}}{{b}}\right)= \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}{ab}}\mathrm{tan}^{−\mathrm{1}} \:\frac{{ab}\sqrt{\mathrm{2}}{t}}{{a}^{\mathrm{2}} {t}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:= \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}{ab}}\mathrm{tan}^{−\mathrm{1}} \:\frac{{ab}\sqrt{\mathrm{2}}\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:{x}\:−{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:{x}}\:+{C} \\ $$
Commented by peter frank last updated on 18/Aug/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by Tawa11 last updated on 20/Aug/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
