
Question Number 17463 by alex041103 last updated on 06/Jul/17
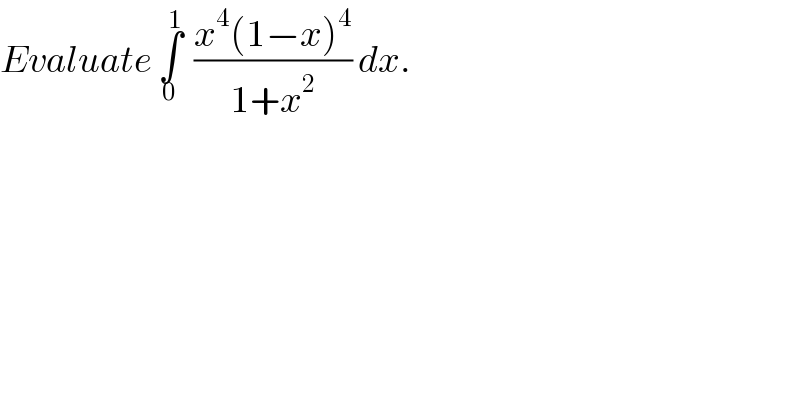
$${Evaluate}\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:\frac{{x}^{\mathrm{4}} \left(\mathrm{1}−{x}\right)^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}. \\ $$
Answered by ajfour last updated on 06/Jul/17

$$\frac{\mathrm{22}}{\mathrm{7}}−\pi\:. \\ $$
Commented by alex041103 last updated on 06/Jul/17
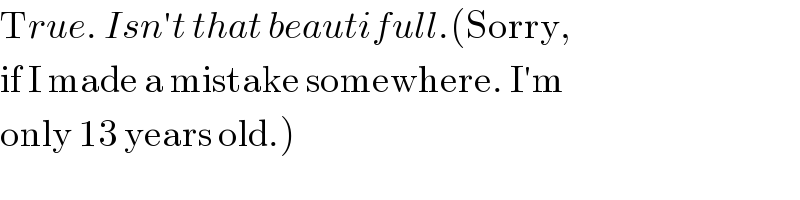
$$\mathrm{T}{rue}.\:{Isn}'{t}\:{that}\:{beautifull}.\left(\mathrm{Sorry},\right. \\ $$$$\mathrm{if}\:\mathrm{I}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{somewhere}.\:\mathrm{I}'\mathrm{m}\: \\ $$$$\left.\mathrm{only}\:\mathrm{13}\:\mathrm{years}\:\mathrm{old}.\right) \\ $$
Commented by ajfour last updated on 06/Jul/17
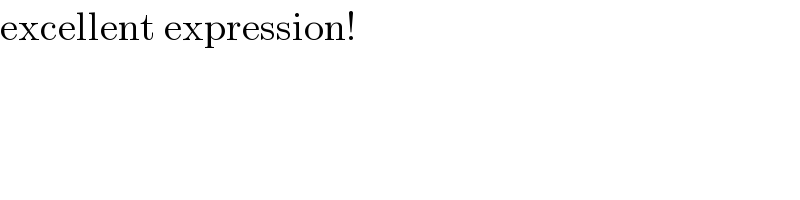
$$\mathrm{excellent}\:\mathrm{expression}!\: \\ $$
Answered by alex041103 last updated on 17/Jul/17
![First (1−x)^4 =1−4x+6x^2 −4x^3 +x^4 We can now do long division x^4 (((1−x)^4 )/(1+x^2 ))=x^4 (x^2 −4x+5−(4/(1+x^2 )))= =x^6 −4x^5 +5x^4 −4(x^4 /(1+x^2 ))= (again long division) =x^6 −4x^5 +5x^4 −4x^2 +4−4(1/(1+x^2 )) And now we integrate and evaluate ⇒∫_0 ^( 1) ((x^4 (1−x)^4 )/(1+x^2 ))dx=((22)/7)−π note: 4∫_0 ^( 1) (1/(1+x^2 ))dx=4[tan^(−1) (x)]_0 ^1 =4(π/4)=π](Q18276.png)
$${First} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{4}} =\mathrm{1}−\mathrm{4}{x}+\mathrm{6}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{3}} +{x}^{\mathrm{4}} \\ $$$${We}\:{can}\:{now}\:{do}\:{long}\:{division} \\ $$$${x}^{\mathrm{4}} \frac{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }={x}^{\mathrm{4}} \left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}−\frac{\mathrm{4}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)= \\ $$$$={x}^{\mathrm{6}} −\mathrm{4}{x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} −\mathrm{4}\frac{{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }=\:\:\:\left({again}\:{long}\:{division}\right) \\ $$$$={x}^{\mathrm{6}} −\mathrm{4}{x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}−\mathrm{4}\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${And}\:{now}\:{we}\:{integrate}\:{and}\:{evaluate} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\mathrm{4}} \left(\mathrm{1}−{x}\right)^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{22}}{\mathrm{7}}−\pi \\ $$$${note}: \\ $$$$\mathrm{4}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\mathrm{4}\left[{tan}^{−\mathrm{1}} \left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{4}\frac{\pi}{\mathrm{4}}=\pi \\ $$
Commented by alex041103 last updated on 18/Jul/17
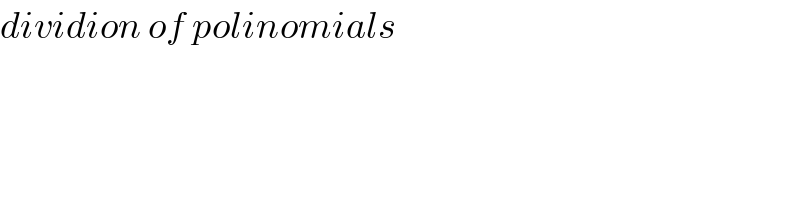
$${dividion}\:{of}\:{polinomials} \\ $$
Commented by alex041103 last updated on 19/Jul/17
$${You}'{ll}\:{dind}\:{some}\:{info}\:{at}\: \\ $$$$\boldsymbol{\mathrm{goo}}.\boldsymbol{\mathrm{gl}}/\boldsymbol{\mathrm{Qo}}\mathrm{7}\boldsymbol{\mathrm{V}}\mathrm{6}\boldsymbol{\mathrm{H}} \\ $$
