
Question Number 1744 by Rasheed Ahmad last updated on 13/Sep/15
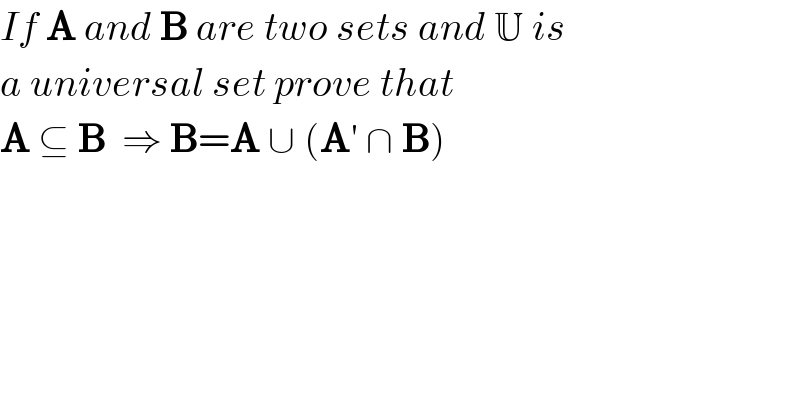
$${If}\:\boldsymbol{\mathrm{A}}\:{and}\:\boldsymbol{\mathrm{B}}\:{are}\:{two}\:{sets}\:{and}\:\mathbb{U}\:{is} \\ $$$${a}\:{universal}\:{set}\:{prove}\:{that} \\ $$$$\boldsymbol{\mathrm{A}}\:\subseteq\:\boldsymbol{\mathrm{B}}\:\:\Rightarrow\:\boldsymbol{\mathrm{B}}=\boldsymbol{\mathrm{A}}\:\cup\:\left(\boldsymbol{\mathrm{A}}'\:\cap\:\boldsymbol{\mathrm{B}}\right) \\ $$
Answered by Rasheed Ahmad last updated on 19/Sep/15
![A ⊆ B ⇒ B=A ∪ (A′ ∩ B) ..........∗∗∗....................... A ⊆ B ⇒A∪B=B Or B=A∪B =U∩(A∪B) [∵ S=U∩S] =(A∪A′)∩(A∪B) [∵U=A∪A′] =A∪(A′∩B) [∵ (A∪B)∩(A∪C) =A∪(B∩C)]](Q1774.png)
$$\boldsymbol{\mathrm{A}}\:\subseteq\:\boldsymbol{\mathrm{B}}\:\:\Rightarrow\:\boldsymbol{\mathrm{B}}=\boldsymbol{\mathrm{A}}\:\cup\:\left(\boldsymbol{\mathrm{A}}'\:\cap\:\boldsymbol{\mathrm{B}}\right) \\ $$$$..........\ast\ast\ast....................... \\ $$$$\boldsymbol{\mathrm{A}}\:\subseteq\:\boldsymbol{\mathrm{B}}\:\:\Rightarrow\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}=\boldsymbol{\mathrm{B}} \\ $$$${Or}\:\:\:\boldsymbol{\mathrm{B}}=\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathbb{U}\cap\left(\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\right)\:\:\:\:\:\left[\because\:\boldsymbol{\mathrm{S}}=\mathbb{U}\cap\boldsymbol{\mathrm{S}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:=\left(\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{A}}'\right)\cap\left(\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\right)\:\:\left[\because\mathbb{U}=\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{A}}'\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\boldsymbol{\mathrm{A}}\cup\left(\boldsymbol{\mathrm{A}}'\cap\boldsymbol{\mathrm{B}}\right)\:\:\:\:\left[\because\:\left(\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\right)\cap\left(\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{C}}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{\mathrm{A}}\cup\left(\boldsymbol{\mathrm{B}}\cap\boldsymbol{\mathrm{C}}\right)\right] \\ $$
Answered by arvind last updated on 18/Sep/15

$$ \\ $$
Answered by Rasheed Soomro last updated on 18/Sep/15
![A ⊆ B ⇒ B=A ∪ (A′ ∩ B) RHS: A ∪ (A′ ∩ B)=(A∪A′)∩(A∪B) [ Distributivity of ∪ over ∩ ] =U∩(A∪B) [ A∪A′=U ] =A∪B [ U ∩ S=S ] =B [ ∵ A⊆B ] =LHS](Q1770.png)
$$\boldsymbol{\mathrm{A}}\:\subseteq\:\boldsymbol{\mathrm{B}}\:\:\Rightarrow\:\boldsymbol{\mathrm{B}}=\boldsymbol{\mathrm{A}}\:\cup\:\left(\boldsymbol{\mathrm{A}}'\:\cap\:\boldsymbol{\mathrm{B}}\right) \\ $$$${RHS}:\:\boldsymbol{\mathrm{A}}\:\cup\:\left(\boldsymbol{\mathrm{A}}'\:\cap\:\boldsymbol{\mathrm{B}}\right)=\left(\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{A}}'\right)\cap\left(\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\left[\:{Distributivity}\:{of}\:\:\:\cup\:\:\:{over}\:\:\:\cap\:\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathbb{U}\cap\left(\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\right)\:\:\:\:\:\left[\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{A}}'=\mathbb{U}\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\:\:\:\:\:\:\:\:\:\:\left[\:\mathbb{U}\:\cap\:\boldsymbol{\mathrm{S}}=\boldsymbol{\mathrm{S}}\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{\mathrm{B}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\:\because\:\boldsymbol{\mathrm{A}}\subseteq\boldsymbol{\mathrm{B}}\:\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={LHS} \\ $$
