
Question Number 173948 by dragan91 last updated on 21/Jul/22
Commented by dragan91 last updated on 21/Jul/22

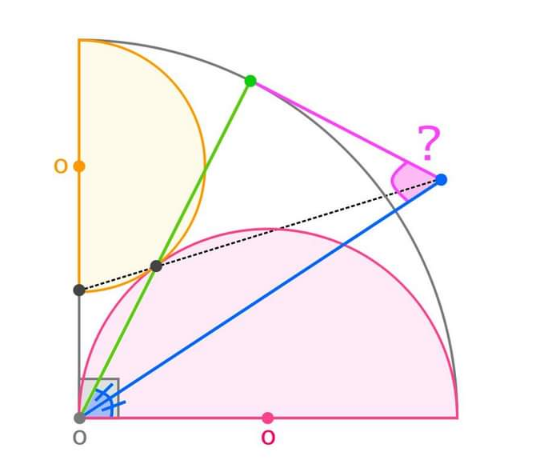
$$\mathrm{Value}\:\mathrm{of}\:\mathrm{Angle}\:? \\ $$
Commented by a.lgnaoui last updated on 22/Jul/22
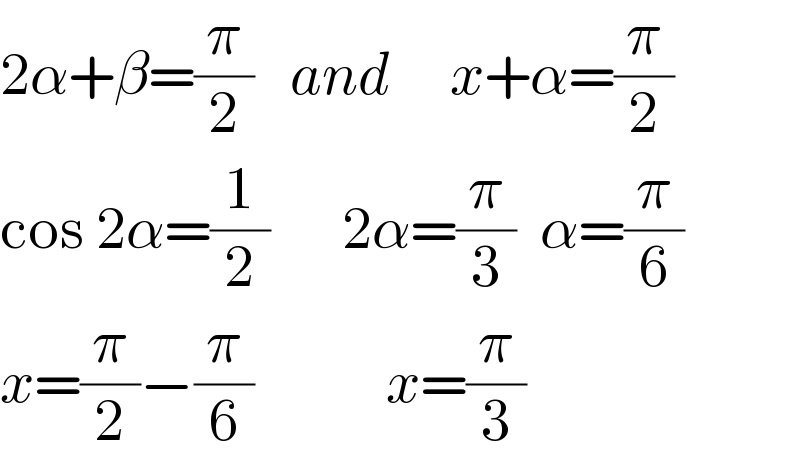
$$\mathrm{2}\alpha+\beta=\frac{\pi}{\mathrm{2}}\:\:\:{and}\:\:\:\:\:{x}+\alpha=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\mathrm{2}\alpha=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\mathrm{2}\alpha=\frac{\pi}{\mathrm{3}}\:\:\alpha=\frac{\pi}{\mathrm{6}} \\ $$$${x}=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{6}}\:\:\:\:\:\:\:\:\:\:\:{x}=\frac{\pi}{\mathrm{3}} \\ $$
Commented by Tawa11 last updated on 22/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 23/Jul/22
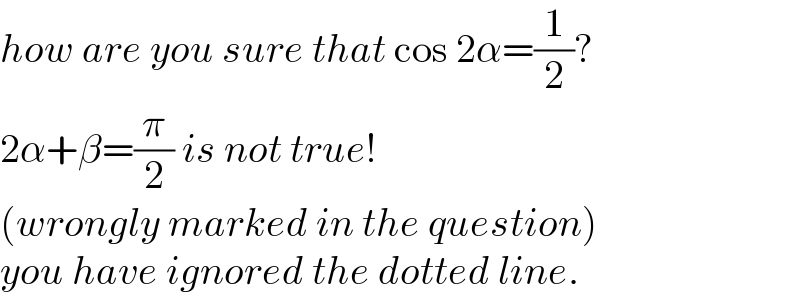
$${how}\:{are}\:{you}\:{sure}\:{that}\:\mathrm{cos}\:\mathrm{2}\alpha=\frac{\mathrm{1}}{\mathrm{2}}? \\ $$$$\mathrm{2}\alpha+\beta=\frac{\pi}{\mathrm{2}}\:{is}\:{not}\:{true}! \\ $$$$\left({wrongly}\:{marked}\:{in}\:{the}\:{question}\right) \\ $$$${you}\:{have}\:{ignored}\:{the}\:{dotted}\:{line}. \\ $$
Answered by mr W last updated on 23/Jul/22

Commented by mr W last updated on 23/Jul/22
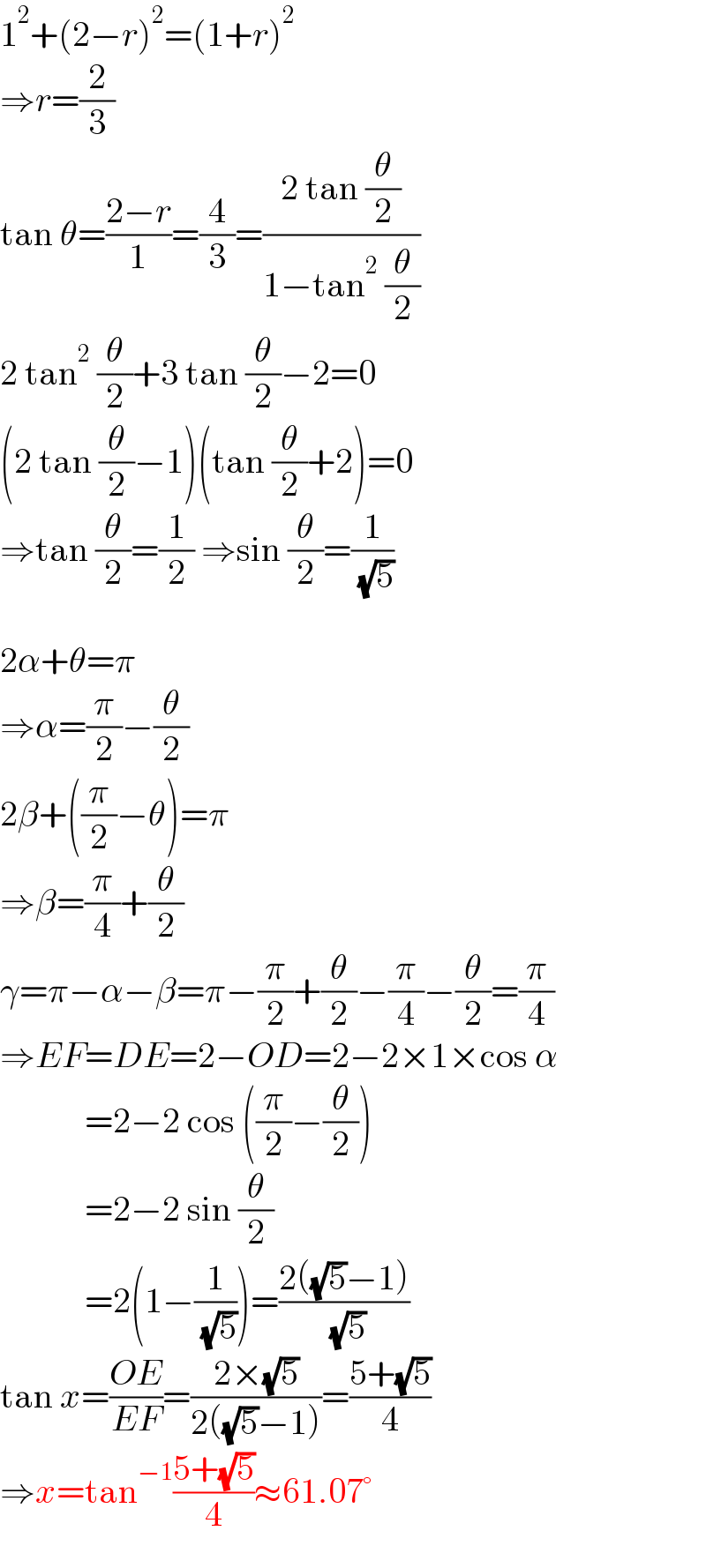
$$\mathrm{1}^{\mathrm{2}} +\left(\mathrm{2}−{r}\right)^{\mathrm{2}} =\left(\mathrm{1}+{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{2}−{r}}{\mathrm{1}}=\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{2}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}} \\ $$$$\mathrm{2}\:\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}+\mathrm{3}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}−\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{2}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{tan}\:\frac{\theta}{\mathrm{2}}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$ \\ $$$$\mathrm{2}\alpha+\theta=\pi \\ $$$$\Rightarrow\alpha=\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{2}\beta+\left(\frac{\pi}{\mathrm{2}}−\theta\right)=\pi \\ $$$$\Rightarrow\beta=\frac{\pi}{\mathrm{4}}+\frac{\theta}{\mathrm{2}} \\ $$$$\gamma=\pi−\alpha−\beta=\pi−\frac{\pi}{\mathrm{2}}+\frac{\theta}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}=\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow{EF}={DE}=\mathrm{2}−{OD}=\mathrm{2}−\mathrm{2}×\mathrm{1}×\mathrm{cos}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}−\mathrm{2}\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}−\mathrm{2}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{tan}\:{x}=\frac{{OE}}{{EF}}=\frac{\mathrm{2}×\sqrt{\mathrm{5}}}{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}=\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}\approx\mathrm{61}.\mathrm{07}° \\ $$
