
Question Number 173532 by 0731619 last updated on 13/Jul/22
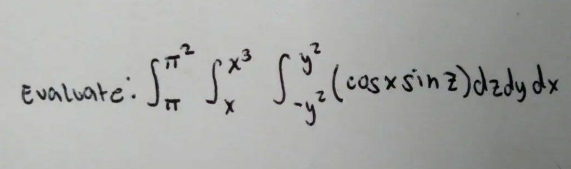
Answered by solvasky last updated on 14/Jul/22
![posons I=∫_π ^π^2 ∫_x ^( x^3 ) ∫_(−y^2 ) ^( y^2 ) cosxsinzdzdydxπ9.π on a I=∫^π^2 _π cosx∫_x ^x^3 ∫_(−y^2 ) ^y^2 sinzdzdydx Comme la fonction f(z)=sinz est impaire alors son integrale sur [−y^(2 ) y^2 ] est nulle et par consequent I=0 Sovalsky★](Q173588.png)
$${posons}\:{I}=\underset{\pi} {\overset{\pi^{\mathrm{2}} } {\int}}\:\underset{{x}} {\overset{\:{x}^{\mathrm{3}} } {\int}}\underset{−{y}^{\mathrm{2}} } {\overset{\:\:\:\:\:\:\:{y}^{\mathrm{2}} } {\int}}{cosxsinzdzdydx}\pi\mathrm{9}.\pi \\ $$$$\:{on}\:{a}\:{I}=\underset{\pi} {\int}^{\pi^{\mathrm{2}} } {cosx}\int_{{x}} ^{{x}^{\mathrm{3}} } \int_{−{y}^{\mathrm{2}} } ^{{y}^{\mathrm{2}} } {sinzdzdydx} \\ $$$$\:{Comme}\:{la}\:{fonction}\:{f}\left({z}\right)={sinz}\:{est}\:{impaire}\:{alors}\:\:{son}\:{integrale}\:{sur}\:\left[−{y}^{\mathrm{2}\:} \:{y}^{\mathrm{2}} \right]\:{est}\:{nulle}\:{et}\:{par}\:{consequent}\:{I}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{Sovalsky}\bigstar \\ $$
