
Question Number 173377 by Shrinava last updated on 10/Jul/22
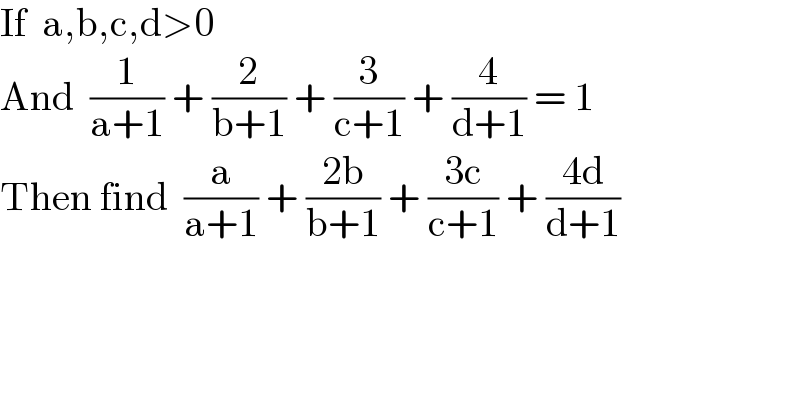
$$\mathrm{If}\:\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}>\mathrm{0} \\ $$ $$\mathrm{And}\:\:\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\:+\:\frac{\mathrm{2}}{\mathrm{b}+\mathrm{1}}\:+\:\frac{\mathrm{3}}{\mathrm{c}+\mathrm{1}}\:+\:\frac{\mathrm{4}}{\mathrm{d}+\mathrm{1}}\:=\:\mathrm{1} \\ $$ $$\mathrm{Then}\:\mathrm{find}\:\:\frac{\mathrm{a}}{\mathrm{a}+\mathrm{1}}\:+\:\frac{\mathrm{2b}}{\mathrm{b}+\mathrm{1}}\:+\:\frac{\mathrm{3c}}{\mathrm{c}+\mathrm{1}}\:+\:\frac{\mathrm{4d}}{\mathrm{d}+\mathrm{1}} \\ $$
Answered by Rasheed.Sindhi last updated on 10/Jul/22

$$\begin{array}{|c|}{\underset{\underset{} {\mathrm{And}\:\:\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\:+\:\frac{\mathrm{2}}{\mathrm{b}+\mathrm{1}}\:+\:\frac{\mathrm{3}}{\mathrm{c}+\mathrm{1}}\:+\:\frac{\mathrm{4}}{\mathrm{d}+\mathrm{1}}\:=\:\mathrm{1}}} {\mathrm{If}\:\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}>\mathrm{0}}}\\\hline\end{array} \\ $$ $$\:\frac{\mathrm{a}}{\mathrm{a}+\mathrm{1}}\:+\:\frac{\mathrm{2b}}{\mathrm{b}+\mathrm{1}}\:+\:\frac{\mathrm{3c}}{\mathrm{c}+\mathrm{1}}\:+\:\frac{\mathrm{4d}}{\mathrm{d}+\mathrm{1}} \\ $$ $$\:=\frac{\mathrm{a}}{\mathrm{a}+\mathrm{1}}−\mathrm{1}\:+\:\frac{\mathrm{2b}}{\mathrm{b}+\mathrm{1}}−\mathrm{2}\:+\:\frac{\mathrm{3c}}{\mathrm{c}+\mathrm{1}}−\mathrm{3}\:+\:\frac{\mathrm{4d}}{\mathrm{d}+\mathrm{1}}−\mathrm{4}+\mathrm{10} \\ $$ $$\:=\frac{−\mathrm{1}}{\mathrm{a}+\mathrm{1}}\:+\:\frac{−\mathrm{2}}{\mathrm{b}+\mathrm{1}}\:+\:\frac{−\mathrm{3}}{\mathrm{c}+\mathrm{1}}\:+\:\frac{−\mathrm{4}}{\mathrm{d}+\mathrm{1}}+\mathrm{10} \\ $$ $$\:=−\left(\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\:+\:\frac{\mathrm{2}}{\mathrm{b}+\mathrm{1}}\:+\:\frac{\mathrm{3}}{\mathrm{c}+\mathrm{1}}\:+\:\frac{\mathrm{4}}{\mathrm{d}+\mathrm{1}}\right)+\mathrm{10} \\ $$ $$=−\left(\mathrm{1}\right)+\mathrm{10}=\mathrm{9} \\ $$
Commented bymr W last updated on 10/Jul/22

$${nice}\:{solution}\:{sir}! \\ $$
Commented byRasheed.Sindhi last updated on 10/Jul/22

$$\mathcal{T}{hanks}\:{a}\:{lot}\:{sir}! \\ $$
Commented byShrinava last updated on 10/Jul/22
$$\mathrm{perfect}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
