
Question Number 173311 by mnjuly1970 last updated on 09/Jul/22

Commented by Rasheed.Sindhi last updated on 09/Jul/22

$$\mathrm{18} \\ $$
Commented by Ar Brandon last updated on 09/Jul/22

$$\mathrm{2088} \\ $$$$\mathrm{2}+\mathrm{0}+\mathrm{8}+\mathrm{8}=\mathrm{18} \\ $$😁
Answered by Ar Brandon last updated on 09/Jul/22

$$#\mathrm{include}\:<\mathrm{stdio}.\mathrm{h}> \\ $$$$ \\ $$$$\mathrm{int}\:\mathrm{main}\left(\mathrm{void}\right) \\ $$$$\left\{\right. \\ $$$$\:\:\:\:\mathrm{for}\:\left(\mathrm{int}\:\mathrm{a}\:=\:\mathrm{1};\:\mathrm{a}\:>\:\mathrm{0};\:\mathrm{a}++\right) \\ $$$$\:\:\:\:\left\{\right. \\ $$$$\:\:\:\:\:\:\:\:\mathrm{if}\:\left(\mathrm{a}\:\%\:\mathrm{29}\:==\:\mathrm{0}\:\&\&\:\mathrm{a}\:\%\:\mathrm{69}\:==\:\mathrm{18}\right) \\ $$$$\:\:\:\:\:\:\:\:\left\{\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{if}\:\left(\mathrm{a}\:/\:\mathrm{1000}\:>\:\mathrm{0}\right)\:\left\{\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{printf}\left(``\%\mathrm{d}'',\:\mathrm{a}\right); \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{break}; \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\right\} \\ $$$$\left.\:\:\:\:\:\:\:\:\right\} \\ $$$$\left.\:\:\:\:\right\} \\ $$$$\:\:\:\:\mathrm{return}\:\mathrm{0}; \\ $$$$\left.\right\}\: \\ $$
Commented by Ar Brandon last updated on 09/Jul/22

$$\mathrm{Output}=\:\mathrm{2088} \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{digits}\:=\:\mathrm{18} \\ $$
Commented by mr W last updated on 09/Jul/22

$${wow}\:{c}^{++} \\ $$
Commented by JDamian last updated on 09/Jul/22
your C code can be improved using for(int a=1000;1;a++)
Commented by Ar Brandon last updated on 09/Jul/22
Yes, Sir !�� That's what I spent my time learning while I was away.
Commented by Ar Brandon last updated on 09/Jul/22
You're right Sir JDamien. Since it consumes unnecessary time testing values of a less than 1000. Thanks for the idea ��
Commented by JDamian last updated on 09/Jul/22
it can be improved further starting the loop with the lowest value for a%29==0, which is 1015, and incrementing a by 29 in each iteration (a+=29). Thus, the check a%29==0 is not needed.
Commented by Ar Brandon last updated on 09/Jul/22
wow! You're right, Sir. That's true. I couldn't think of that so quickly.
Commented by Ar Brandon last updated on 09/Jul/22
#include <stdio.h> int main(void) { int a; for (a = 1015; a % 69 != 18; a += 29); printf("%d", a); return 0; }
Commented by Tawa11 last updated on 11/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Jul/22

$${According}\:{to}\:{first}\:{condition}: \\ $$$$\:\:\:\:{Let}\:{the}\:{required}\:{number}\:{is}\:\:\mathrm{29}{m} \\ $$$${Applying}\:\:{second}\:{condition}: \\ $$$$\mathrm{29}{m}\equiv\mathrm{18}\left({mod}\:\mathrm{69}\right) \\ $$$${Process}: \\ $$$$\mathrm{29}{m}\equiv\mathrm{18}+\mathrm{69}=\mathrm{87}\left({mod}\:\mathrm{69}\right) \\ $$$${m}\equiv\mathrm{3}\left({mod}\:\mathrm{69}\right)\: \\ $$$${The}\:{number}\:{is}\:\mathrm{29}{m}=\mathrm{29}\left(\mathrm{3}\right)=\mathrm{87} \\ $$$${But}\:{this}\:{number}\:{is}\:{not}\:{of}\:\mathrm{4}-{digit} \\ $$$${Next}\:{such}\:{number}\:{will}\:{be}: \\ $$$$ \\ $$$${m}\equiv\mathrm{3}+\mathrm{69}=\mathrm{72}\left({mod}\:\mathrm{69}\right) \\ $$$$\therefore\mathrm{29}{m}=\mathrm{29}×\mathrm{72}=\mathrm{2088}\:\left(\mathrm{4}-{digit}\right) \\ $$$$ \\ $$$${Sum}\:{of}\:{digits}: \\ $$$$\mathrm{2}+\mathrm{0}+\mathrm{8}+\mathrm{8}=\mathrm{18} \\ $$
Answered by mr W last updated on 09/Jul/22
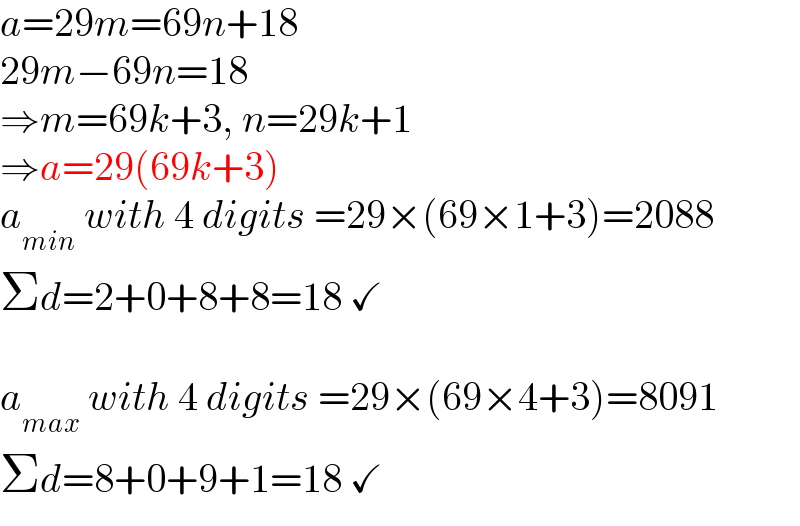
$${a}=\mathrm{29}{m}=\mathrm{69}{n}+\mathrm{18} \\ $$$$\mathrm{29}{m}−\mathrm{69}{n}=\mathrm{18} \\ $$$$\Rightarrow{m}=\mathrm{69}{k}+\mathrm{3},\:{n}=\mathrm{29}{k}+\mathrm{1} \\ $$$$\Rightarrow{a}=\mathrm{29}\left(\mathrm{69}{k}+\mathrm{3}\right) \\ $$$${a}_{{min}} \:{with}\:\mathrm{4}\:{digits}\:=\mathrm{29}×\left(\mathrm{69}×\mathrm{1}+\mathrm{3}\right)=\mathrm{2088} \\ $$$$\Sigma{d}=\mathrm{2}+\mathrm{0}+\mathrm{8}+\mathrm{8}=\mathrm{18}\:\checkmark \\ $$$$ \\ $$$${a}_{{max}} \:{with}\:\mathrm{4}\:{digits}\:=\mathrm{29}×\left(\mathrm{69}×\mathrm{4}+\mathrm{3}\right)=\mathrm{8091} \\ $$$$\Sigma{d}=\mathrm{8}+\mathrm{0}+\mathrm{9}+\mathrm{1}=\mathrm{18}\:\checkmark \\ $$
Answered by Raxreedoroid last updated on 09/Jul/22

$$\mathrm{9999}\geqslant{a}>\mathrm{999} \\ $$$${a}=\mathrm{29}{n}_{\mathrm{1}} \\ $$$${a}=\mathrm{69}{n}_{\mathrm{2}} +\mathrm{18} \\ $$$${a}=\left(\mathrm{69}×\mathrm{29}\right){n}+\mathrm{29}{k} \\ $$$${a}=\mathrm{2001}{n}+\mathrm{29}{k},\:{n}\:\mathrm{is}\:\mathrm{a}\:\mathrm{free}\:\mathrm{variable}. \\ $$$$\mathrm{smallest}\:\mathrm{value}\:\mathrm{of}\:{a}\:\mathrm{is}\:\mathrm{at}\:{n}=\mathrm{1} \\ $$$${a}=\mathrm{29}{k}+\mathrm{2001} \\ $$$$\mathrm{29}{k}\equiv\mathrm{18}\:\left(\mathrm{mod}\:\mathrm{69}\right) \\ $$$$\mathrm{29}{k}\equiv\mathrm{87}\:\left(\mathrm{mod}\:\mathrm{69}\right) \\ $$$${k}\equiv\mathrm{3}\:\left(\mathrm{mod}\:\mathrm{69}\right) \\ $$$${k}=\mathrm{3} \\ $$$${a}=\mathrm{87}+\mathrm{2001}=\mathrm{2088} \\ $$
