
Question Number 173309 by mathlove last updated on 09/Jul/22
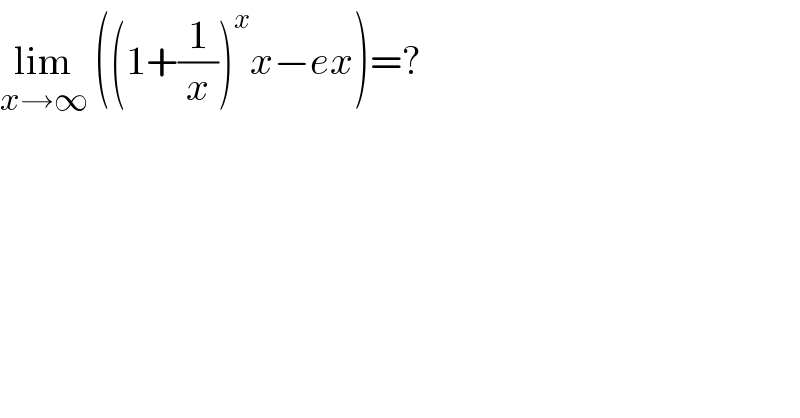
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} {x}−{ex}\right)=? \\ $$
Answered by CElcedricjunior last updated on 12/Jul/22
![lim_(x→∞) [(1+(1/x))^x x−ex]=+∞−∞=FI posons (1/x)=X⇔x=(1/X) qd:x→∞;X→0 lim_(x→0) [(((1+X)^(1/X) −e)/X)]=lim_(x→0) ((e^((ln(1+X))/X) −e)/X) dl ((ln(x+1))/x)=1−(x/2)+X^2 𝛏(x) lim_(x→0) 𝛏(x)=0 dl e^u =e+e(u−1)+(u−1)σ(x) avec lim_(x→1) σ(x)=0 e^((ln(1+x))/x) =e+e(−(x/2))+𝛏(x) lim_(x→0) 𝛏(x)=0 lim_(x→0) ((e^((ln(x+1))/x) −e)/x)=lim_(x→0) ((e−(e/2)x−e+𝛏(x))/x) =lim_(x→0) −((ex)/(2x)) =lim_(x→0) ((−e)/2) lim_(x→∞) [(1+(1/x))^x x−xe]=−(e/2) ..........le ce^� le^� bre cedric junior............](Q173483.png)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)^{\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{ex}}\right]=+\infty−\infty=\boldsymbol{\mathrm{FI}} \\ $$$$\boldsymbol{\mathrm{posons}}\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}=\boldsymbol{\mathrm{X}}\Leftrightarrow\boldsymbol{\mathrm{x}}=\frac{\mathrm{1}}{\boldsymbol{\mathrm{X}}} \\ $$$$\boldsymbol{\mathrm{qd}}:\boldsymbol{\mathrm{x}}\rightarrow\infty;\boldsymbol{\mathrm{X}}\rightarrow\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\left(\mathrm{1}+\boldsymbol{\mathrm{X}}\right)^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{X}}}} −\boldsymbol{\mathrm{e}}}{\boldsymbol{\mathrm{X}}}\right]=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{e}}^{\frac{\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\boldsymbol{\mathrm{X}}\right)}{\boldsymbol{\mathrm{X}}}} −\boldsymbol{\mathrm{e}}}{\boldsymbol{\mathrm{X}}} \\ $$$$\boldsymbol{\mathrm{dl}}\:\frac{\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right)}{\boldsymbol{\mathrm{x}}}=\mathrm{1}−\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}+\boldsymbol{\mathrm{X}}^{\mathrm{2}} \boldsymbol{\xi}\left(\boldsymbol{\mathrm{x}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\boldsymbol{\xi}\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{dl}}\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{u}}} =\boldsymbol{\mathrm{e}}+\boldsymbol{\mathrm{e}}\left(\boldsymbol{\mathrm{u}}−\mathrm{1}\right)+\left(\boldsymbol{\mathrm{u}}−\mathrm{1}\right)\sigma\left(\boldsymbol{\mathrm{x}}\right) \\ $$$$\boldsymbol{\mathrm{avec}}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\sigma\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{e}}^{\frac{\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}}} =\boldsymbol{\mathrm{e}}+\boldsymbol{\mathrm{e}}\left(−\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}\right)+\boldsymbol{\xi}\left(\boldsymbol{\mathrm{x}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\boldsymbol{\xi}\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{e}}^{\frac{\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right)}{\boldsymbol{\mathrm{x}}}} −\boldsymbol{\mathrm{e}}}{\boldsymbol{\mathrm{x}}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{e}}−\frac{\boldsymbol{\mathrm{e}}}{\mathrm{2}}\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{e}}+\boldsymbol{\xi}\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}} \\ $$$$\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{\boldsymbol{\mathrm{ex}}}{\mathrm{2}\boldsymbol{\mathrm{x}}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\boldsymbol{\mathrm{e}}}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)^{\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{xe}}\right]=−\frac{\boldsymbol{\mathrm{e}}}{\mathrm{2}} \\ $$$$\: \\ $$$$\:..........{le}\:{c}\acute {{e}l}\grave {{e}bre}\:{cedric}\:{junior}............ \\ $$
Commented by mathlove last updated on 13/Jul/22

$${a}\:{lot}\:{thanks} \\ $$
Answered by mr W last updated on 09/Jul/22
![=lim_(x→∞) [(1+(1/x))^x −e]x =lim_(x→0) (((1+x)^(1/x) −e)/x) =lim_(x→0) ((e−((ex)/2)+((11ex^2 )/(24))+o(x^3 )−e)/x) =−(e/2) ✓](Q173345.png)
$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} −{e}\right]{x} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} −{e}}{{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}−\frac{{ex}}{\mathrm{2}}+\frac{\mathrm{11}{ex}^{\mathrm{2}} }{\mathrm{24}}+{o}\left({x}^{\mathrm{3}} \right)−{e}}{{x}} \\ $$$$=−\frac{{e}}{\mathrm{2}}\:\checkmark \\ $$
Commented by mathlove last updated on 10/Jul/22

$${thanks}\:{mr}\:{W} \\ $$
Commented by Tawa11 last updated on 11/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
