
Question Number 17260 by Umar math last updated on 03/Jul/17
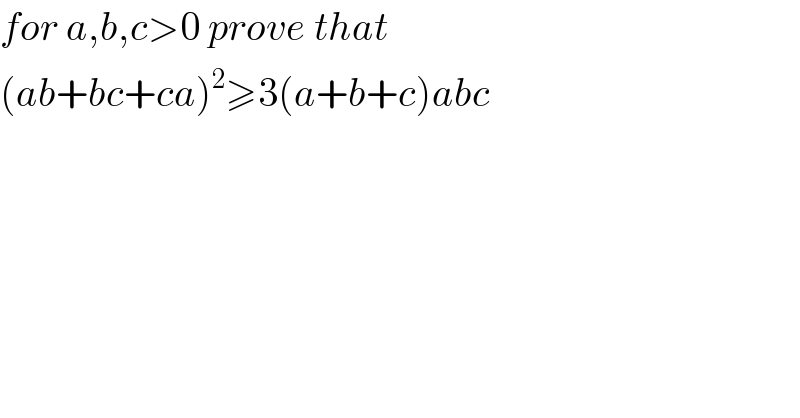
$${for}\:{a},{b},{c}>\mathrm{0}\:{prove}\:{that} \\ $$ $$\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} \geqslant\mathrm{3}\left({a}+{b}+{c}\right){abc} \\ $$
Commented byprakash jain last updated on 03/Jul/17
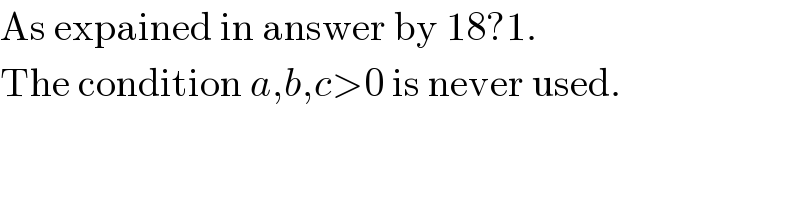
$$\mathrm{As}\:\mathrm{expained}\:\mathrm{in}\:\mathrm{answer}\:\mathrm{by}\:\mathrm{18}?\mathrm{1}. \\ $$ $$\mathrm{The}\:\mathrm{condition}\:{a},{b},{c}>\mathrm{0}\:\mathrm{is}\:\mathrm{never}\:\mathrm{used}. \\ $$
Answered by 18±1 last updated on 05/Jul/17
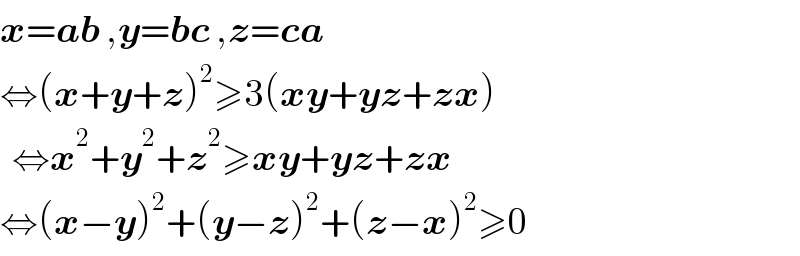
$$\boldsymbol{{x}}=\boldsymbol{{ab}}\:,\boldsymbol{{y}}=\boldsymbol{{bc}}\:,\boldsymbol{{z}}=\boldsymbol{{ca}} \\ $$ $$\Leftrightarrow\left(\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}\right)^{\mathrm{2}} \geqslant\mathrm{3}\left(\boldsymbol{{xy}}+\boldsymbol{{yz}}+\boldsymbol{{zx}}\right) \\ $$ $$\:\:\Leftrightarrow\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{z}}^{\mathrm{2}} \geqslant\boldsymbol{{xy}}+\boldsymbol{{yz}}+\boldsymbol{{zx}} \\ $$ $$\Leftrightarrow\left(\boldsymbol{{x}}−\boldsymbol{{y}}\right)^{\mathrm{2}} +\left(\boldsymbol{{y}}−\boldsymbol{{z}}\right)^{\mathrm{2}} +\left(\boldsymbol{{z}}−\boldsymbol{{x}}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$
Commented by18±1 last updated on 03/Jul/17
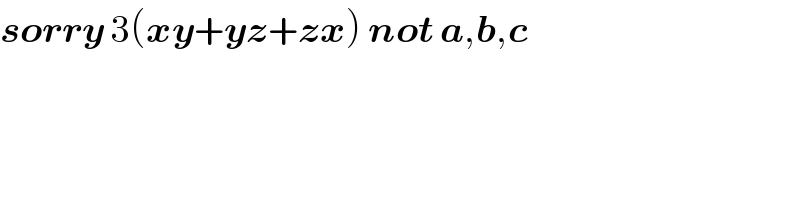
$$\boldsymbol{{sorry}}\:\mathrm{3}\left(\boldsymbol{{xy}}+\boldsymbol{{yz}}+\boldsymbol{{zx}}\right)\:\boldsymbol{{not}}\:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}} \\ $$
Commented byUmar math last updated on 03/Jul/17
$${thank}\:{you}\:{sir},\:{but}\:{am}\:{kind}\:{of}\:{confused}. \\ $$
Commented by1234Hello last updated on 03/Jul/17
$$\mathrm{I}\:\mathrm{am}\:\mathrm{in}\:\mathrm{doubt}\:\mathrm{that}\:\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:\mathrm{proved} \\ $$ $$\mathrm{or}\:\mathrm{not}?! \\ $$
Commented byprakash jain last updated on 03/Jul/17
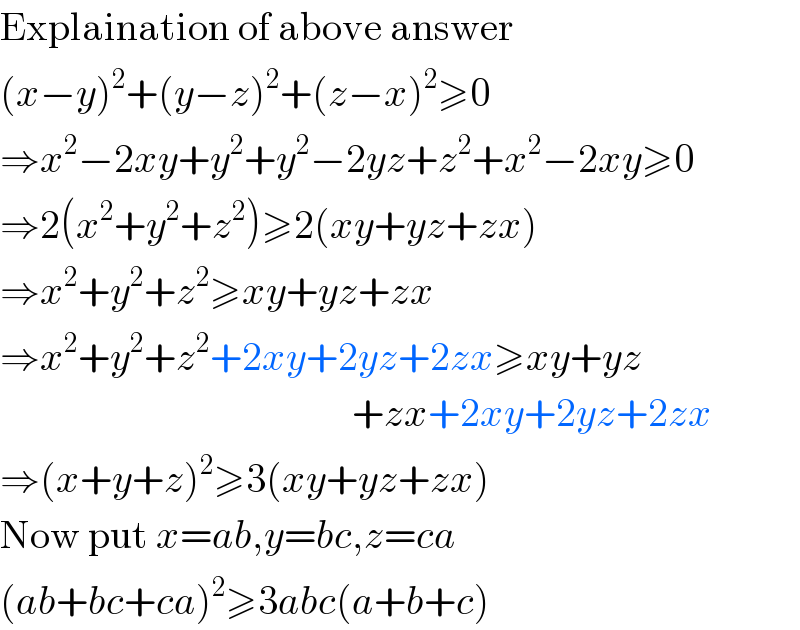
$$\mathrm{Explaination}\:\mathrm{of}\:\mathrm{above}\:\mathrm{answer} \\ $$ $$\left({x}−{y}\right)^{\mathrm{2}} +\left({y}−{z}\right)^{\mathrm{2}} +\left({z}−{x}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$ $$\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{xy}+{y}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{yz}+{z}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{xy}\geqslant\mathrm{0} \\ $$ $$\Rightarrow\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)\geqslant\mathrm{2}\left({xy}+{yz}+{zx}\right) \\ $$ $$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \geqslant{xy}+{yz}+{zx} \\ $$ $$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{2}{yz}+\mathrm{2}{zx}\geqslant{xy}+{yz} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{zx}+\mathrm{2}{xy}+\mathrm{2}{yz}+\mathrm{2}{zx} \\ $$ $$\Rightarrow\left({x}+{y}+{z}\right)^{\mathrm{2}} \geqslant\mathrm{3}\left({xy}+{yz}+{zx}\right) \\ $$ $$\mathrm{Now}\:\mathrm{put}\:{x}={ab},{y}={bc},{z}={ca} \\ $$ $$\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} \geqslant\mathrm{3}{abc}\left({a}+{b}+{c}\right) \\ $$
Commented byUmar math last updated on 03/Jul/17
$${thanks}\:{a}\:{bunch}\:{sir},\:{am}\:{clear}\:{know} \\ $$
Commented byTinkutara last updated on 04/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
