
Question Number 171552 by 0731619 last updated on 17/Jun/22
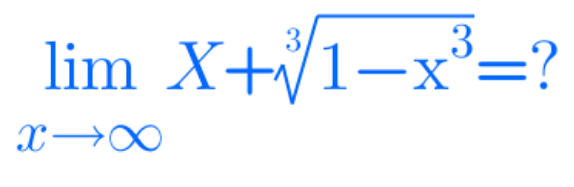
Answered by alephzero last updated on 17/Jun/22
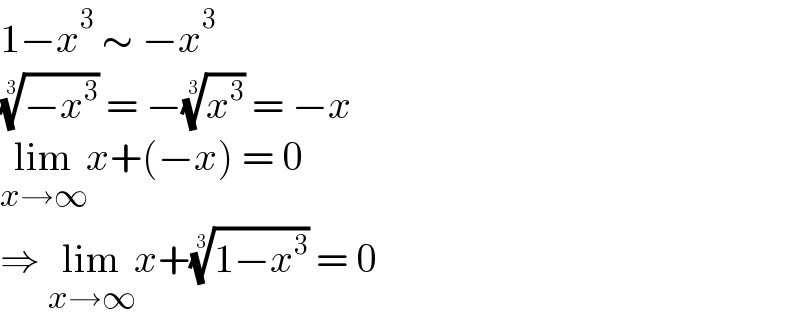
$$\mathrm{1}−{x}^{\mathrm{3}} \:\sim\:−{x}^{\mathrm{3}} \\ $$$$\sqrt[{\mathrm{3}}]{−{x}^{\mathrm{3}} }\:=\:−\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} }\:=\:−{x} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{x}+\left(−{x}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{x}+\sqrt[{\mathrm{3}}]{\mathrm{1}−{x}^{\mathrm{3}} }\:=\:\mathrm{0} \\ $$
Answered by Mathematification last updated on 17/Jun/22
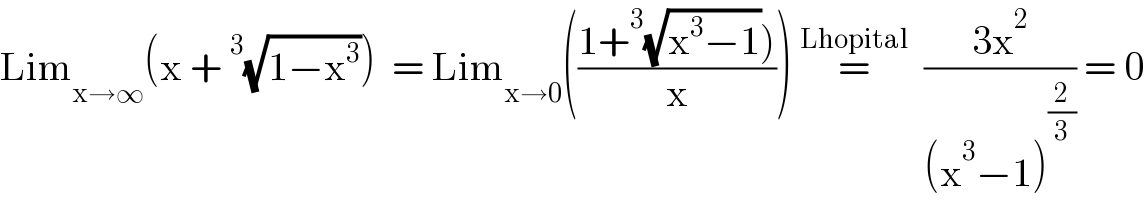
$$\mathrm{Lim}_{\mathrm{x}\rightarrow\infty} \left(\mathrm{x}\:+\:^{\mathrm{3}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{3}} }\right)\:\:=\:\mathrm{Lim}_{\mathrm{x}\rightarrow\mathrm{0}} \left(\frac{\left.\mathrm{1}+^{\mathrm{3}} \sqrt{\mathrm{x}^{\mathrm{3}} −\mathrm{1}}\right)}{\mathrm{x}}\right)\:\overset{\mathrm{Lhopital}} {=}\:\:\frac{\mathrm{3x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} }\:=\:\mathrm{0} \\ $$
