
Question Number 171549 by Shrinava last updated on 17/Jun/22
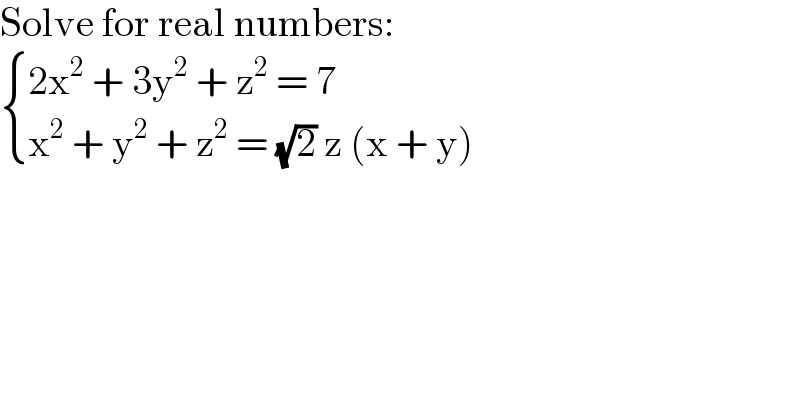
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\begin{cases}{\mathrm{2x}^{\mathrm{2}} \:+\:\mathrm{3y}^{\mathrm{2}} \:+\:\mathrm{z}^{\mathrm{2}} \:=\:\mathrm{7}}\\{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} \:+\:\mathrm{z}^{\mathrm{2}} \:=\:\sqrt{\mathrm{2}}\:\mathrm{z}\:\left(\mathrm{x}\:+\:\mathrm{y}\right)}\end{cases} \\ $$
Answered by MJS_new last updated on 21/Jun/22
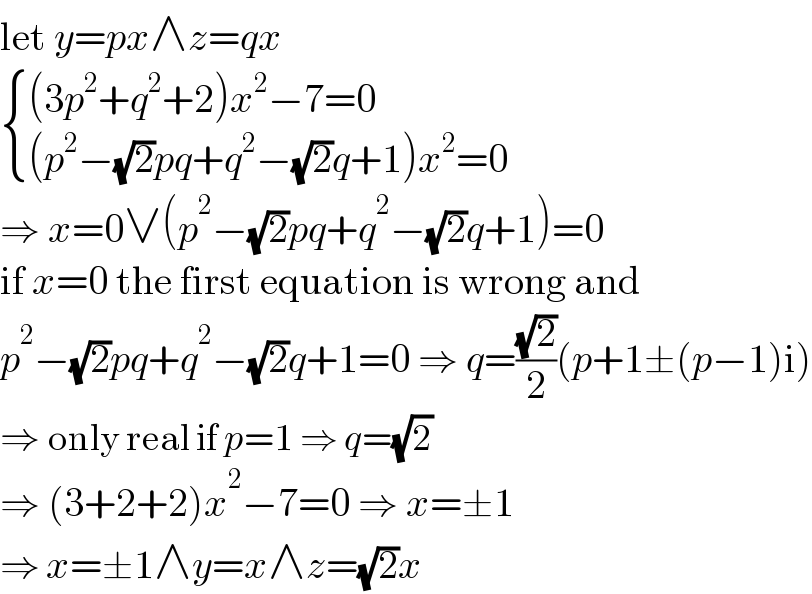
$$\mathrm{let}\:{y}={px}\wedge{z}={qx} \\ $$$$\begin{cases}{\left(\mathrm{3}{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +\mathrm{2}\right){x}^{\mathrm{2}} −\mathrm{7}=\mathrm{0}}\\{\left({p}^{\mathrm{2}} −\sqrt{\mathrm{2}}{pq}+{q}^{\mathrm{2}} −\sqrt{\mathrm{2}}{q}+\mathrm{1}\right){x}^{\mathrm{2}} =\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\:{x}=\mathrm{0}\vee\left({p}^{\mathrm{2}} −\sqrt{\mathrm{2}}{pq}+{q}^{\mathrm{2}} −\sqrt{\mathrm{2}}{q}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{if}\:{x}=\mathrm{0}\:\mathrm{the}\:\mathrm{first}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{and} \\ $$$${p}^{\mathrm{2}} −\sqrt{\mathrm{2}}{pq}+{q}^{\mathrm{2}} −\sqrt{\mathrm{2}}{q}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:{q}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left({p}+\mathrm{1}\pm\left({p}−\mathrm{1}\right)\mathrm{i}\right) \\ $$$$\Rightarrow\:\mathrm{only}\:\mathrm{real}\:\mathrm{if}\:{p}=\mathrm{1}\:\Rightarrow\:{q}=\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\:\left(\mathrm{3}+\mathrm{2}+\mathrm{2}\right){x}^{\mathrm{2}} −\mathrm{7}=\mathrm{0}\:\Rightarrow\:{x}=\pm\mathrm{1} \\ $$$$\Rightarrow\:{x}=\pm\mathrm{1}\wedge{y}={x}\wedge{z}=\sqrt{\mathrm{2}}{x} \\ $$
