
Question Number 171455 by mokys last updated on 15/Jun/22
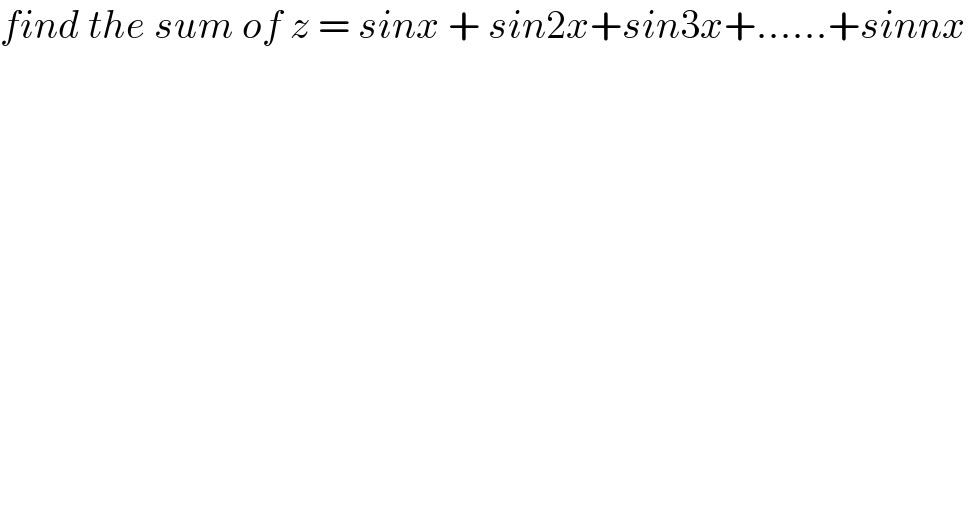
$${find}\:{the}\:{sum}\:{of}\:{z}\:=\:{sinx}\:+\:{sin}\mathrm{2}{x}+{sin}\mathrm{3}{x}+......+{sinnx}\: \\ $$
Commented by mr W last updated on 15/Jun/22
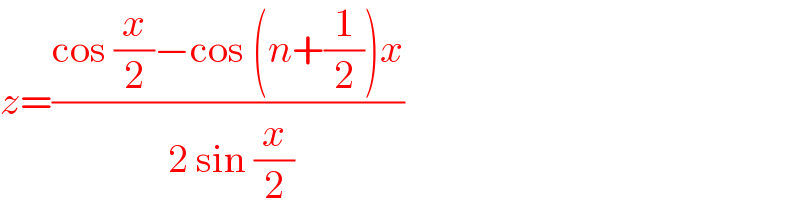
$${z}=\frac{\mathrm{cos}\:\frac{{x}}{\mathrm{2}}−\mathrm{cos}\:\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\:\mathrm{2}\:\mathrm{sin}\:\frac{{x}}{\mathrm{2}}} \\ $$
Answered by mr W last updated on 16/Jun/22
)/((cos x−1+i sin x)(cos x−1−i sin x))) A+iB=(([cos (n+1)x−1](cos x−1)+sin (n+1)x sin x+i{sin (n+1)x (cos x−1)−[cos (n+1)x−1]sin x})/( 4 sin^2 (x/2))) ⇒A=(([cos (n+1)x−1](cos x−1)+sin (n+1)x sin x)/( 4 sin^2 (x/2))) ⇒A=((sin (n+(1/2))x−sin (x/2))/( 2 sin (x/2))) B=((sin (n+1)x (cos x−1)−[cos (n+1)x−1]sin x)/( 4 sin^2 (x/2))) ⇒B=((cos (x/2)−cos (n+(1/2))x)/( 2 sin (x/2)))](Q171462.png)
$${let}\:{A}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}\:{kx} \\ $$$${let}\:{B}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{sin}\:{kx} \\ $$$${A}+{iB}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{cos}\:{kx}+{i}\:\mathrm{sin}\:{kx}\right) \\ $$$${A}+{iB}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{{ikx}} =\frac{{e}^{{i}\left({n}+\mathrm{1}\right){x}} −\mathrm{1}}{{e}^{{ix}} −\mathrm{1}} \\ $$$${A}+{iB}=\frac{\mathrm{cos}\:\left({n}+\mathrm{1}\right){x}−\mathrm{1}+{i}\:\mathrm{sin}\:\left({n}+\mathrm{1}\right){x}}{\mathrm{cos}\:{x}−\mathrm{1}+{i}\:\mathrm{sin}\:{x}} \\ $$$${A}+{iB}=\frac{\left[\mathrm{cos}\:\left({n}+\mathrm{1}\right){x}−\mathrm{1}+{i}\:\mathrm{sin}\:\left({n}+\mathrm{1}\right){x}\right]\left(\mathrm{cos}\:{x}−\mathrm{1}−{i}\:\mathrm{sin}\:{x}\right)}{\left(\mathrm{cos}\:{x}−\mathrm{1}+{i}\:\mathrm{sin}\:{x}\right)\left(\mathrm{cos}\:{x}−\mathrm{1}−{i}\:\mathrm{sin}\:{x}\right)} \\ $$$${A}+{iB}=\frac{\left[\mathrm{cos}\:\left({n}+\mathrm{1}\right){x}−\mathrm{1}\right]\left(\mathrm{cos}\:{x}−\mathrm{1}\right)+\mathrm{sin}\:\left({n}+\mathrm{1}\right){x}\:\mathrm{sin}\:{x}+{i}\left\{\mathrm{sin}\:\left({n}+\mathrm{1}\right){x}\:\left(\mathrm{cos}\:{x}−\mathrm{1}\right)−\left[\mathrm{cos}\:\left({n}+\mathrm{1}\right){x}−\mathrm{1}\right]\mathrm{sin}\:{x}\right\}}{\:\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}} \\ $$$$\Rightarrow{A}=\frac{\left[\mathrm{cos}\:\left({n}+\mathrm{1}\right){x}−\mathrm{1}\right]\left(\mathrm{cos}\:{x}−\mathrm{1}\right)+\mathrm{sin}\:\left({n}+\mathrm{1}\right){x}\:\mathrm{sin}\:{x}}{\:\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}} \\ $$$$\Rightarrow{A}=\frac{\mathrm{sin}\:\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}−\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}{\:\mathrm{2}\:\mathrm{sin}\:\frac{{x}}{\mathrm{2}}} \\ $$$${B}=\frac{\mathrm{sin}\:\left({n}+\mathrm{1}\right){x}\:\left(\mathrm{cos}\:{x}−\mathrm{1}\right)−\left[\mathrm{cos}\:\left({n}+\mathrm{1}\right){x}−\mathrm{1}\right]\mathrm{sin}\:{x}}{\:\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}} \\ $$$$\Rightarrow{B}=\frac{\mathrm{cos}\:\frac{{x}}{\mathrm{2}}−\mathrm{cos}\:\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\:\mathrm{2}\:\mathrm{sin}\:\frac{{x}}{\mathrm{2}}} \\ $$
