
Question Number 17095 by Tinkutara last updated on 30/Jun/17
![The total number of solutions of the equation tan x + sec x = 2 which lie in the interval [0, 2π] is](Q17095.png)
$$\mathrm{The}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\mathrm{tan}\:{x}\:+\:\mathrm{sec}\:{x}\:=\:\mathrm{2}\:\mathrm{which}\:\mathrm{lie}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{interval}\:\left[\mathrm{0},\:\mathrm{2}\pi\right]\:\mathrm{is} \\ $$
Answered by sma3l2996 last updated on 30/Jun/17
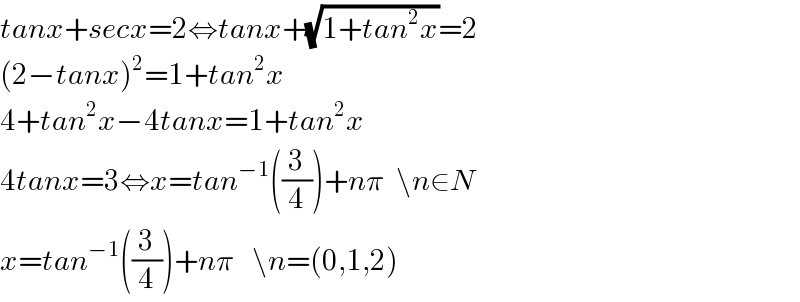
$${tanx}+{secx}=\mathrm{2}\Leftrightarrow{tanx}+\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {x}}=\mathrm{2} \\ $$$$\left(\mathrm{2}−{tanx}\right)^{\mathrm{2}} =\mathrm{1}+{tan}^{\mathrm{2}} {x} \\ $$$$\mathrm{4}+{tan}^{\mathrm{2}} {x}−\mathrm{4}{tanx}=\mathrm{1}+{tan}^{\mathrm{2}} {x} \\ $$$$\mathrm{4}{tanx}=\mathrm{3}\Leftrightarrow{x}={tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)+{n}\pi\:\:\backslash{n}\in{N} \\ $$$${x}={tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)+{n}\pi\:\:\:\backslash{n}=\left(\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$
Commented by Tinkutara last updated on 01/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Commented by ajfour last updated on 01/Jul/17
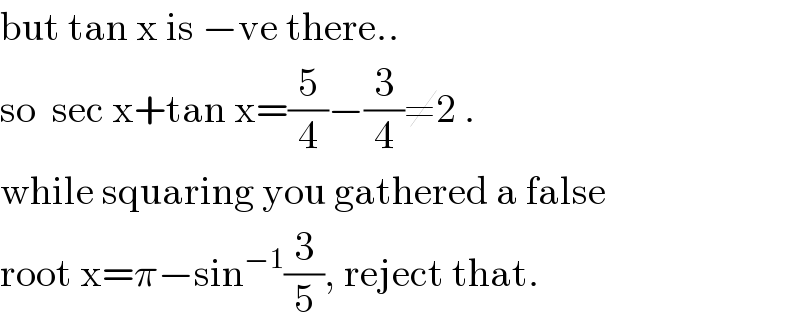
$$\mathrm{but}\:\mathrm{tan}\:\mathrm{x}\:\mathrm{is}\:−\mathrm{ve}\:\mathrm{there}.. \\ $$$$\mathrm{so}\:\:\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}=\frac{\mathrm{5}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{4}}\neq\mathrm{2}\:. \\ $$$$\mathrm{while}\:\mathrm{squaring}\:\mathrm{you}\:\mathrm{gathered}\:\mathrm{a}\:\mathrm{false} \\ $$$$\mathrm{root}\:\mathrm{x}=\pi−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{5}},\:\mathrm{reject}\:\mathrm{that}. \\ $$
Commented by sma3l2996 last updated on 01/Jul/17
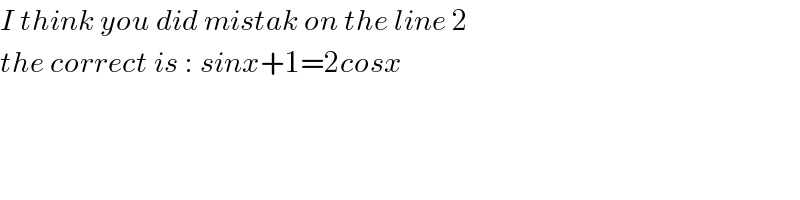
$${I}\:{think}\:{you}\:{did}\:{mistak}\:{on}\:{the}\:{line}\:\mathrm{2} \\ $$$${the}\:{correct}\:{is}\::\:{sinx}+\mathrm{1}=\mathrm{2}{cosx} \\ $$
Commented by ajfour last updated on 01/Jul/17
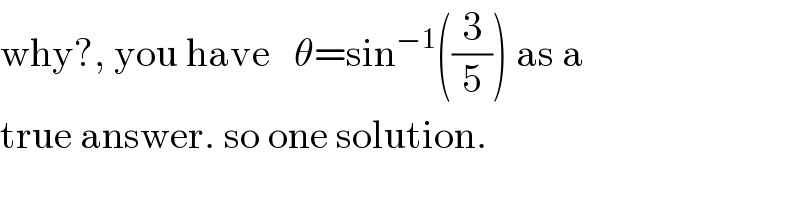
$$\mathrm{why}?,\:\mathrm{you}\:\mathrm{have}\:\:\:\theta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{5}}\right)\:\mathrm{as}\:\mathrm{a} \\ $$$$\mathrm{true}\:\mathrm{answer}.\:\mathrm{so}\:\mathrm{one}\:\mathrm{solution}. \\ $$
