
Question Number 170458 by MathsFan last updated on 24/May/22
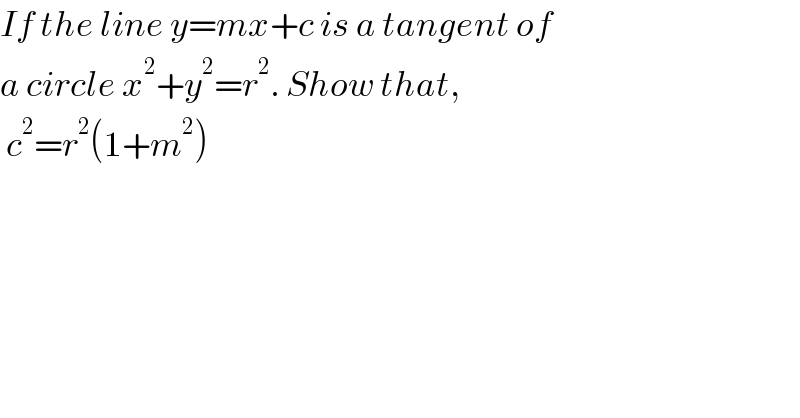
$${If}\:{the}\:{line}\:{y}={mx}+{c}\:{is}\:{a}\:{tangent}\:{of} \\ $$$${a}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} .\:{Show}\:{that},\: \\ $$$$\:{c}^{\mathrm{2}} ={r}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right) \\ $$
Answered by greougoury555 last updated on 24/May/22
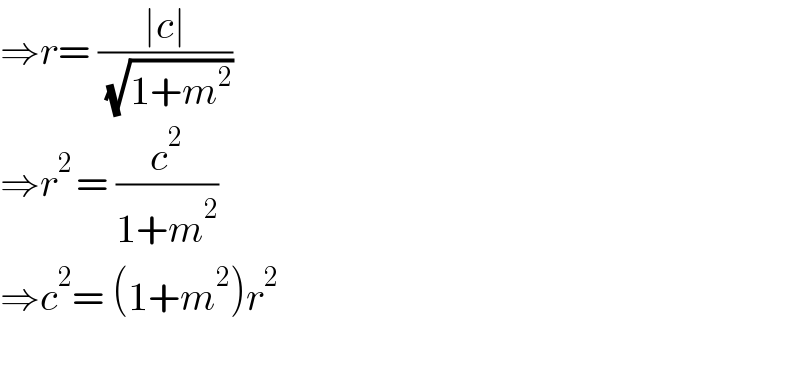
$$\Rightarrow{r}=\:\frac{\mid{c}\mid}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }} \\ $$$$\Rightarrow{r}^{\mathrm{2}\:} =\:\frac{{c}^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\Rightarrow{c}^{\mathrm{2}} =\:\left(\mathrm{1}+{m}^{\mathrm{2}} \right){r}^{\mathrm{2}} \\ $$$$ \\ $$
Commented by MathsFan last updated on 24/May/22

$${thank}\:{you}\:{sir} \\ $$
