
Question Number 170117 by mathlove last updated on 16/May/22
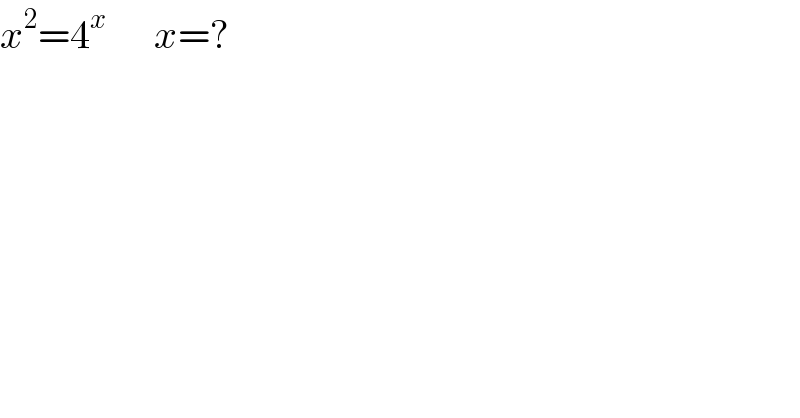
$${x}^{\mathrm{2}} =\mathrm{4}^{{x}} \:\:\:\:\:\:{x}=? \\ $$$$ \\ $$$$ \\ $$
Commented by mathlove last updated on 16/May/22
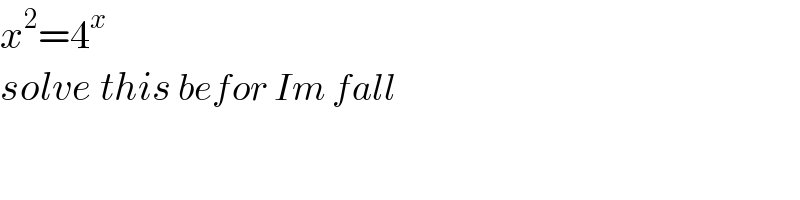
$${x}^{\mathrm{2}} =\mathrm{4}^{{x}} \\ $$$${solve}\:{this}\:{befor}\:{Im}\:{fall} \\ $$
Answered by mr W last updated on 16/May/22
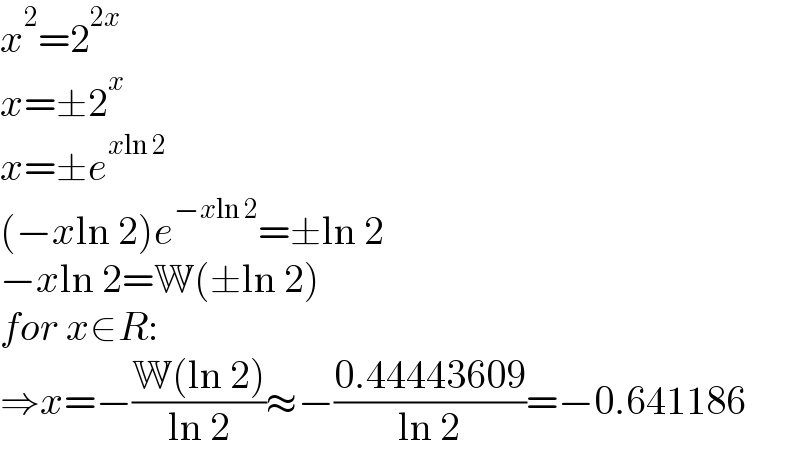
$${x}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}{x}} \\ $$$${x}=\pm\mathrm{2}^{{x}} \\ $$$${x}=\pm{e}^{{x}\mathrm{ln}\:\mathrm{2}} \\ $$$$\left(−{x}\mathrm{ln}\:\mathrm{2}\right){e}^{−{x}\mathrm{ln}\:\mathrm{2}} =\pm\mathrm{ln}\:\mathrm{2} \\ $$$$−{x}\mathrm{ln}\:\mathrm{2}=\mathbb{W}\left(\pm\mathrm{ln}\:\mathrm{2}\right) \\ $$$${for}\:{x}\in{R}: \\ $$$$\Rightarrow{x}=−\frac{\mathbb{W}\left(\mathrm{ln}\:\mathrm{2}\right)}{\mathrm{ln}\:\mathrm{2}}\approx−\frac{\mathrm{0}.\mathrm{44443609}}{\mathrm{ln}\:\mathrm{2}}=−\mathrm{0}.\mathrm{641186} \\ $$
Commented by mathlove last updated on 17/May/22

$${thanks}\: \\ $$
