
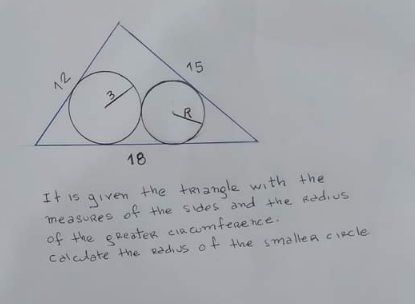
Question Number 169088 by cortano1 last updated on 24/Apr/22
Answered by mr W last updated on 24/Apr/22
![a=18 b=15 c=12 s=(18+15+12)/2=22.5 Δ=(√(22.5×4.5×7.5×10.5))=((135(√7))/4) sin B=((2Δ)/(ac))=((2×135(√7))/(4×18×12))=((5(√7))/(16)) ⇒cos B=(9/(16)) sin C=((2Δ)/(ab))=((2×135(√7))/(4×18×15))=((√7)/4) ⇒cos C=(3/4) tan (B/2)=(((5(√7))/(16))/(1+(9/(16))))=((√7)/5) tan (C/2)=(((√7)/4)/(1+(3/4)))=((√7)/7) (18−(3/(tan (B/2)))−(R/(tan (C/2))))^2 =(3+R)^2 −(3−R)^2 (18−((15(√7))/( 7))−(√7)R)^2 =12R (18−((15(√7))/( 7)))^2 −18(2(√7)−1)R+7R^2 =0 R=(1/7)[9(2(√7)−1)−(√(81(2(√7)−1)^2 −7(18−((15(√7))/( 7)))^2 ))] =((9(2(√7)−1)−6(√(2(3(√7)−2))))/7)≈2.564](Q169095.png)
$${a}=\mathrm{18} \\ $$$${b}=\mathrm{15} \\ $$$${c}=\mathrm{12} \\ $$$${s}=\left(\mathrm{18}+\mathrm{15}+\mathrm{12}\right)/\mathrm{2}=\mathrm{22}.\mathrm{5} \\ $$$$\Delta=\sqrt{\mathrm{22}.\mathrm{5}×\mathrm{4}.\mathrm{5}×\mathrm{7}.\mathrm{5}×\mathrm{10}.\mathrm{5}}=\frac{\mathrm{135}\sqrt{\mathrm{7}}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:{B}=\frac{\mathrm{2}\Delta}{{ac}}=\frac{\mathrm{2}×\mathrm{135}\sqrt{\mathrm{7}}}{\mathrm{4}×\mathrm{18}×\mathrm{12}}=\frac{\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{16}}\:\Rightarrow\mathrm{cos}\:{B}=\frac{\mathrm{9}}{\mathrm{16}} \\ $$$$\mathrm{sin}\:{C}=\frac{\mathrm{2}\Delta}{{ab}}=\frac{\mathrm{2}×\mathrm{135}\sqrt{\mathrm{7}}}{\mathrm{4}×\mathrm{18}×\mathrm{15}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}\:\Rightarrow\mathrm{cos}\:{C}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{tan}\:\frac{{B}}{\mathrm{2}}=\frac{\frac{\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{16}}}{\mathrm{1}+\frac{\mathrm{9}}{\mathrm{16}}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{5}} \\ $$$$\mathrm{tan}\:\frac{{C}}{\mathrm{2}}=\frac{\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{7}} \\ $$$$\left(\mathrm{18}−\frac{\mathrm{3}}{\mathrm{tan}\:\frac{{B}}{\mathrm{2}}}−\frac{{R}}{\mathrm{tan}\:\frac{{C}}{\mathrm{2}}}\right)^{\mathrm{2}} =\left(\mathrm{3}+{R}\right)^{\mathrm{2}} −\left(\mathrm{3}−{R}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{18}−\frac{\mathrm{15}\sqrt{\mathrm{7}}}{\:\mathrm{7}}−\sqrt{\mathrm{7}}{R}\right)^{\mathrm{2}} =\mathrm{12}{R} \\ $$$$\left(\mathrm{18}−\frac{\mathrm{15}\sqrt{\mathrm{7}}}{\:\mathrm{7}}\right)^{\mathrm{2}} −\mathrm{18}\left(\mathrm{2}\sqrt{\mathrm{7}}−\mathrm{1}\right){R}+\mathrm{7}{R}^{\mathrm{2}} =\mathrm{0} \\ $$$${R}=\frac{\mathrm{1}}{\mathrm{7}}\left[\mathrm{9}\left(\mathrm{2}\sqrt{\mathrm{7}}−\mathrm{1}\right)−\sqrt{\mathrm{81}\left(\mathrm{2}\sqrt{\mathrm{7}}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{7}\left(\mathrm{18}−\frac{\mathrm{15}\sqrt{\mathrm{7}}}{\:\mathrm{7}}\right)^{\mathrm{2}} }\right] \\ $$$$\:\:\:=\frac{\mathrm{9}\left(\mathrm{2}\sqrt{\mathrm{7}}−\mathrm{1}\right)−\mathrm{6}\sqrt{\mathrm{2}\left(\mathrm{3}\sqrt{\mathrm{7}}−\mathrm{2}\right)}}{\mathrm{7}}\approx\mathrm{2}.\mathrm{564} \\ $$
Commented by mr W last updated on 24/Apr/22

Commented by Tawa11 last updated on 24/Apr/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
