
Question Number 168906 by cortano1 last updated on 21/Apr/22

Answered by mr W last updated on 21/Apr/22
![tan (B/2)=((b/c)/(1+(a/c)))=(b/(a+c))=(b/(a+(√(a^2 +b^2 )))) tan (A/2)=((a/c)/(1+(b/c)))=(a/(b+c))=(a/(b+(√(a^2 +b^2 )))) (r/(tan (B/2)))+(r/(tan (A/2)))+(n−1)r=c=(√(a^2 +b^2 )) r[((a+(√(a^2 +b^2 )))/b)+((b+(√(a^2 +b^2 )))/a)+n−1]=(√(a^2 +b^2 )) ⇒r=((√(a^2 +b^2 ))/(((a+(√(a^2 +b^2 )))/b)+((b+(√(a^2 +b^2 )))/a)+n−1))](Q168931.png)
$$\mathrm{tan}\:\frac{{B}}{\mathrm{2}}=\frac{\frac{{b}}{{c}}}{\mathrm{1}+\frac{{a}}{{c}}}=\frac{{b}}{{a}+{c}}=\frac{{b}}{{a}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\frac{{A}}{\mathrm{2}}=\frac{\frac{{a}}{{c}}}{\mathrm{1}+\frac{{b}}{{c}}}=\frac{{a}}{{b}+{c}}=\frac{{a}}{{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\frac{{r}}{\mathrm{tan}\:\frac{{B}}{\mathrm{2}}}+\frac{{r}}{\mathrm{tan}\:\frac{{A}}{\mathrm{2}}}+\left({n}−\mathrm{1}\right){r}={c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${r}\left[\frac{{a}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{b}}+\frac{{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{a}}+{n}−\mathrm{1}\right]=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{r}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\frac{{a}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{b}}+\frac{{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{a}}+{n}−\mathrm{1}} \\ $$
Commented by Tawa11 last updated on 21/Apr/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by cortano1 last updated on 22/Apr/22

$${waw}...{great} \\ $$
Commented by peter frank last updated on 26/Apr/22
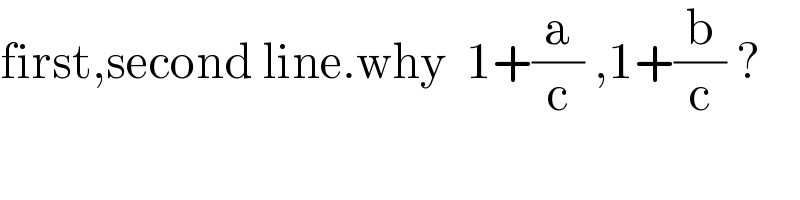
$$\mathrm{first},\mathrm{second}\:\mathrm{line}.\mathrm{why}\:\:\mathrm{1}+\frac{\mathrm{a}}{\mathrm{c}}\:,\mathrm{1}+\frac{\mathrm{b}}{\mathrm{c}}\:? \\ $$
Commented by mr W last updated on 26/Apr/22

$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta} \\ $$
